Ols lasso

Nous travaillons sur la base de données diabetes de python. La base initiale comporte n = 442 patients et p = 10 covariables. La variable Y à expliquer est un score correspondant à l’évolution de la maladie. Pour s’amuser, un robot malicieux a contaminé le jeu de données en y ajoutant 200 variables explicatives inappropriées. Ensuite, non-content d’avoir déjà perverti notre jeu de données, il a volontairement mélangé les variables entre elle de façon aléatoire. Bien entendu le robot a ensuite pris soin d’effacer toute trace de son acte crapuleux si bien que nous ne connaissons pas les variables pertinentes. La nouvelle base de données comporte n = 442 patients et p = 210 covariables, notés X. Saurez-vous déjouer les plans de ce robot farceur et retrouver les variables pertinentes ?

Importer la base de données data_dm3.csv disponible depuis le lien https://bitbucket. org/portierf/shared_files/downloads/data_dm3.csv. La dernière colonne est la va- riable à expliquer. Les autres colonnes sont les variables explicatives. Préciser le nombre de variables explicatives et le nombre d’observations.

import pandas as pd
import numpy as np
import time
import matplotlib.pyplot as plt
from matplotlib import rc
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn import linear_model
from sklearn.preprocessing import StandardScaler
import scipy.stats as stat
import statsmodels.api as sm
from sklearn import preprocessing
from sklearn import linear_model
from sklearn.preprocessing import StandardScaler, PolynomialFeatures
from numpy.linalg import svd
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
from mpl_toolkits.mplot3d import Axes3D
from sklearn.model_selection import KFold
from sklearn.linear_model import LassoCV
from sklearn.datasets import make_regression
%matplotlib inline

data = pd.read_csv('/Users/yang/Downloads/data_dm3.csv', sep=',', header=None)

data.head()

	0	1	2	3	4	5	6	7	8	9	...	201	202	203	204	205	206	207	208	209	210
0	-1.298173	-0.162249	1.223379	1.355554	1.080171	0.634979	0.298741	0.548270	0.731773	1.018645	...	0.588278	0.210106	1.861458	-0.436399	0.279299	-1.416020	-2.332363	0.215096	-0.693319	151.0
1	0.166951	-0.338060	-0.618867	0.759366	1.134281	-0.536844	-0.075120	0.970251	-0.327487	0.717310	...	-0.251054	-0.825716	0.339139	1.119430	0.225958	-0.822288	0.382838	-0.718829	-0.188993	75.0
2	-0.416177	-0.205659	-1.282226	1.675500	1.523746	0.192029	-0.235840	-1.954626	-0.853309	0.892791	...	1.283837	0.372516	-0.652557	-2.579347	0.139267	-1.901196	0.048210	0.220205	0.471588	141.0
3	0.867184	-0.398667	0.093501	0.025971	1.852099	0.789774	0.801775	0.376711	0.853689	0.247953	...	0.446582	0.334733	0.399074	-0.884172	0.723819	1.316367	0.088218	0.619496	1.061662	206.0
4	1.193282	-0.936980	-0.725039	0.766078	0.223489	-1.584622	1.146866	0.086136	-0.088780	-0.945066	...	0.786157	-1.058179	-0.155788	-0.642504	2.040010	-1.703110	-1.901502	1.778811	-0.489853	135.0

5 rows × 211 columns

le nombre de variables explicatives est 211 et le nombre d’observations est 1.

Les variables explicatives sont-elles centrées? Normalisées? Qu’en est-il de la variable à expliquer ? Tracer un scatter plot de la base de données avec 4 covariables prises au hasard et la variable à expliquer (un scatterplot regroupe les graphes de chacune des variables en fonction de chacune des autres). Commenter les graphiques obtenus.

data.iloc[:,0:10].mean()

  7.535450e-19
 -1.507090e-17
  5.494599e-20
 -7.284269e-18
  8.288995e-18
 -2.712762e-17
  1.971776e-17
  8.540177e-18
  1.029845e-17
  4.018907e-18
dtype: float64

les variables explicatives sont centrées

data.iloc[:,0:10].var(ddof=0)

  1.0
  1.0
  1.0
  1.0
  1.0
  1.0
  1.0
  1.0
  1.0
  1.0
dtype: float64

les variables explicatives sont normalisées

data.iloc[:,-1].mean()

152.13348416289594

data.iloc[:,-1].var()

5943.331347923785

La variable à expliquer n’est pas centrée normalisée.

plt.figure()

random4index = np.random.randint(0, 209, size=4)
X = data[random4index]
y = data.iloc[:, -1]

# sns.pairplot(X,y)

plt.figure(figsize=(20, 10))

index = np.append(random4index, 210)
# xy=pd.concat(X,y,axis=1)
pd.plotting.scatter_matrix(data[index])
plt.ylabel('x', fontsize=18)

plt.xlabel('', fontsize=18)
plt.title('Matplot scatter plot')
plt.legend(loc=2)
plt.show()

No handles with labels found to put in legend.

<Figure size 432x288 with 0 Axes>

<Figure size 1440x720 with 0 Axes>

png

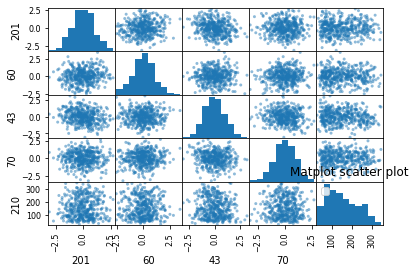
sns.pairplot(data[index],diag_kind='kde')

<seaborn.axisgrid.PairGrid at 0x1c1f63ce48>

png

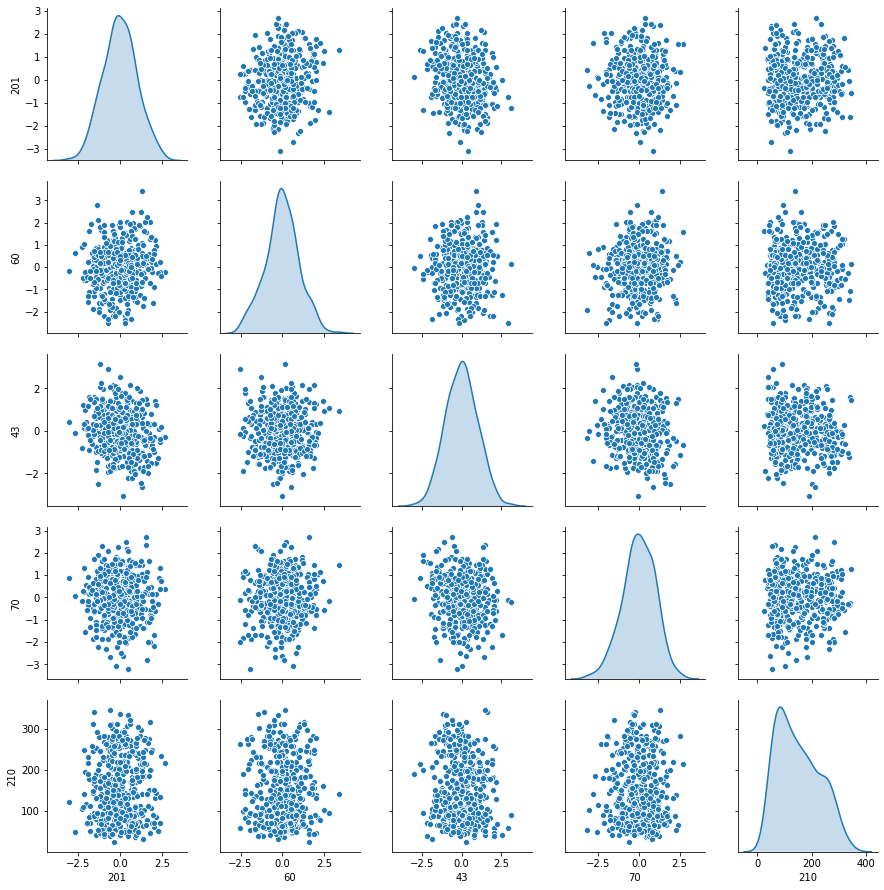
Les variables explicatives me semble sous distribution normal.
Les variables explicatives sont indépendents entre eux.
pas de corrélations significatives entre xi et y

3. Echantillon d’apprentissage et de test. Créer 2 échantillons : un pour apprendre le modèle Xtrain, un pour tester le modèle Xtest. On mettra 20% de la base dans l’échantillon ’test’. Donner les tailles de chacun des 2 échantillons. On notera que le nouvel échantillon de covariables Xtrain n’est pas normalizé. Dans la suite, on fera donc bien attention à inclure l’intercept dans nos régression.

Xtrain, Xtest, ytrain, ytest = train_test_split(
    data.iloc[:, :210], data.iloc[:, -1], test_size=0.2,random_state=88)
print('Xtrain:', np.shape(Xtrain))
print('Xtest:', np.shape(Xtest))

Xtrain: (353, 210)
Xtest: (89, 210)

Xtrain.iloc[:,0:10].mean()

 -0.020106
  0.036134
  0.007141
  0.004181
 -0.009112
  0.001871
  0.038508
  0.008441
  0.015847
 -0.013114
dtype: float64

Xtrain.iloc[:,0:10].var()

  1.045122
  0.983220
  1.021202
  1.037738
  1.046602
  1.018488
  1.018648
  0.994559
  0.990711
  1.039069
dtype: float64

échantillon Xtrain n’est ni centré ni normalisé, mais cela n’est pas évident de voir sur les graphs

Xytrain = pd.concat([Xtrain, ytrain], axis=1)
sns.pairplot(Xytrain[index], diag_kind='kde')

<seaborn.axisgrid.PairGrid at 0x1c2093ccf8>

png

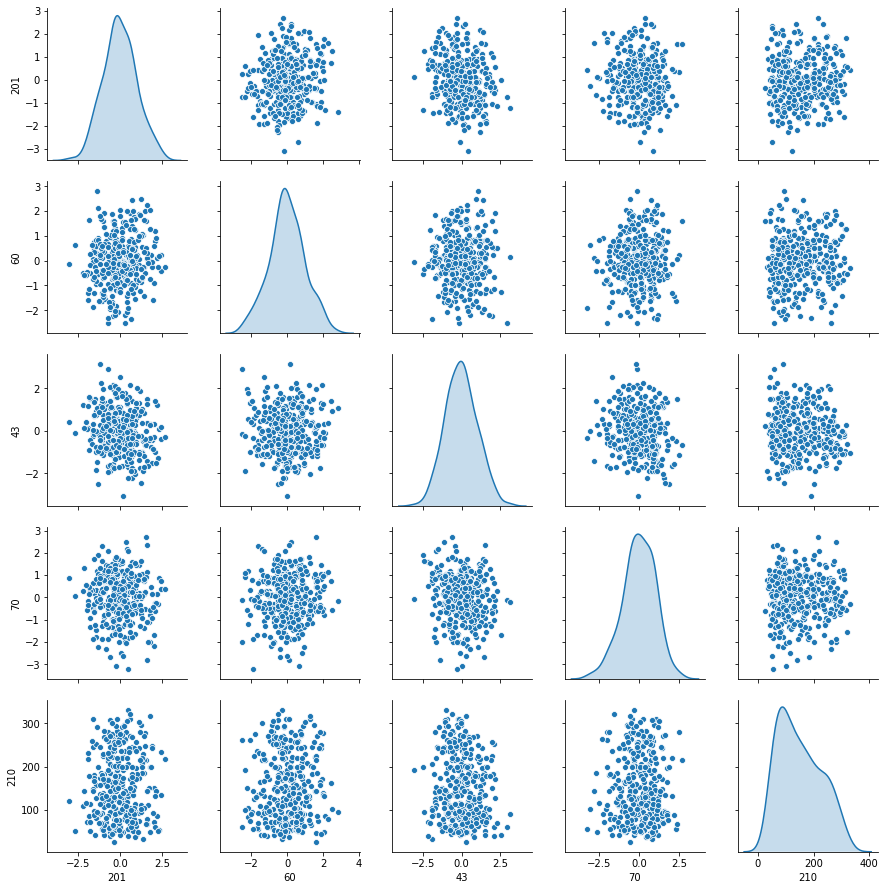
4. Donner la matrice de covariance calculée sur Xtrain. Tracer le graphe de la décroissance des valeurs propres de la matrice de covariance (ou de corrélation). Expliquer pourquoi il est légitime de ne garder que les premières variables de l’ACP. On gardera 60 variables dans la suite

# covariance matrice
# have to scale first if compute manully : X- np.mean(X) /np.std(X)
np.cov(Xtrain)

array([[ 0.99316073,  0.06094896, -0.18412495, ..., -0.03292253,
         0.00839064,  0.10516165],
       [ 0.06094896,  0.71086166, -0.04691278, ..., -0.05380649,
        -0.00193438,  0.03514817],
       [-0.18412495, -0.04691278,  1.02764869, ...,  0.04934272,
         0.1826571 , -0.02595332],
       ...,
       [-0.03292253, -0.05380649,  0.04934272, ...,  1.02904151,
         0.00815779, -0.02076334],
       [ 0.00839064, -0.00193438,  0.1826571 , ...,  0.00815779,
         0.84537331, -0.00378885],
       [ 0.10516165,  0.03514817, -0.02595332, ..., -0.02076334,
        -0.00378885,  0.91335404]])

#use sklearn SVD -- X.T
v, s, u = np.linalg.svd(np.cov(Xtrain.T))
s  # eigen values

array([5.70589881e+00, 5.32462615e+00, 5.19573490e+00, 5.11505778e+00,
       5.06831132e+00, 5.02122530e+00, 4.95501010e+00, 4.88119854e+00,
       4.85924981e+00, 4.81750868e+00, 4.76488619e+00, 4.73245279e+00,
       4.67949329e+00, 4.63802652e+00, 4.59567631e+00, 4.58284319e+00,
       4.50301942e+00, 4.45520574e+00, 4.42094099e+00, 4.39508602e+00,
       4.34778652e+00, 4.30591223e+00, 4.28190997e+00, 4.21696843e+00,
       4.16534807e+00, 4.10653922e+00, 4.07261904e+00, 3.98592279e+00,
       3.93253001e+00, 3.85567803e+00, 3.82665585e+00, 3.78249643e+00,
       3.73443823e+00, 3.66458698e+00, 3.60881730e+00, 3.59490393e+00,
       3.56065992e+00, 3.49756455e+00, 3.39326793e+00, 3.33218139e+00,
       3.25259250e+00, 3.22671109e+00, 3.19252915e+00, 3.06931369e+00,
       2.96248587e+00, 2.90320055e+00, 2.85079290e+00, 2.74084037e+00,
       2.70780914e+00, 2.53732705e+00, 2.31460987e+00, 1.23699361e+00,
       1.00063357e+00, 7.95129729e-01, 5.86771301e-01, 4.86781929e-01,
       4.31273134e-01, 3.67008585e-01, 6.80119617e-02, 7.62016201e-03,
       5.06785618e-15, 4.45495788e-15, 2.94660065e-15, 2.92093653e-15,
       2.84432059e-15, 2.70462918e-15, 2.57908885e-15, 2.50121581e-15,
       2.33756661e-15, 2.32973799e-15, 2.25909529e-15, 2.20160953e-15,
       2.09043376e-15, 2.04529300e-15, 1.93984091e-15, 1.92274461e-15,
       1.90945924e-15, 1.88117582e-15, 1.85091449e-15, 1.78386269e-15,
       1.76666204e-15, 1.73249635e-15, 1.69587279e-15, 1.68356022e-15,
       1.65588379e-15, 1.65155330e-15, 1.57171589e-15, 1.56566405e-15,
       1.53850787e-15, 1.50789870e-15, 1.49527601e-15, 1.47786896e-15,
       1.45799281e-15, 1.43055208e-15, 1.39915673e-15, 1.35561458e-15,
       1.32953552e-15, 1.28622503e-15, 1.27431871e-15, 1.26029235e-15,
       1.24343096e-15, 1.21363591e-15, 1.19197960e-15, 1.16341565e-15,
       1.15183729e-15, 1.15170207e-15, 1.12233543e-15, 1.10356424e-15,
       1.08991616e-15, 1.06798045e-15, 1.04891696e-15, 1.02505056e-15,
       1.01722513e-15, 1.01022013e-15, 9.86014409e-16, 9.74283613e-16,
       9.71505352e-16, 9.63815157e-16, 9.60171920e-16, 9.30534772e-16,
       9.18315199e-16, 9.09752243e-16, 9.02344053e-16, 8.91019783e-16,
       8.57759590e-16, 8.49938714e-16, 8.44234222e-16, 8.32285079e-16,
       8.18601531e-16, 8.07500788e-16, 7.93195348e-16, 7.78142361e-16,
       7.60699162e-16, 7.42068988e-16, 7.30847568e-16, 7.09348641e-16,
       7.00784128e-16, 6.78633952e-16, 6.77611301e-16, 6.56329334e-16,
       6.35835836e-16, 6.17998058e-16, 5.97739489e-16, 5.91414985e-16,
       5.87361080e-16, 5.67992642e-16, 5.53702600e-16, 5.34515352e-16,
       5.30737099e-16, 5.01900306e-16, 4.80735537e-16, 4.55993052e-16,
       4.49523825e-16, 4.29566640e-16, 4.16843865e-16, 4.12704888e-16,
       4.12704888e-16, 4.12704888e-16, 4.12704888e-16, 4.12704888e-16,
       4.12704888e-16, 4.12704888e-16, 4.12704888e-16, 4.12704888e-16,
       4.12704888e-16, 4.12704888e-16, 4.12704888e-16, 4.12704888e-16,
       4.12704888e-16, 4.12704888e-16, 4.12704888e-16, 4.12704888e-16,
       4.12704888e-16, 4.12704888e-16, 4.12704888e-16, 4.12704888e-16,
       4.12704888e-16, 4.12704888e-16, 4.12704888e-16, 4.12704888e-16,
       4.12704888e-16, 4.12704888e-16, 4.12704888e-16, 4.12704888e-16,
       4.12704888e-16, 4.12704888e-16, 4.12704888e-16, 4.12704888e-16,
       4.12704888e-16, 4.05049589e-16, 3.87937802e-16, 3.65820487e-16,
       3.34125203e-16, 3.13071900e-16, 2.91431293e-16, 2.65519042e-16,
       2.65345673e-16, 2.51361398e-16, 2.43024941e-16, 2.10836308e-16,
       2.03392001e-16, 1.93634585e-16, 1.78716181e-16, 1.70564671e-16,
       1.44609916e-16, 1.16967424e-16, 9.44014684e-17, 5.17450508e-17,
       3.43236481e-17, 7.14057503e-18])

np.cov(Xtrain.T).shape

(210, 210)

# plot eigen values
plt.scatter(range(len(s)),s)

<matplotlib.collections.PathCollection at 0x1c235017f0>

png

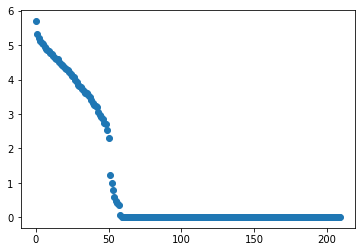
On voit bien sur le graphique que lorsque nous somme dans la base des vecteurs propres de $X^TX$, seulement 60 des valeurs propres de la matrice de corrélation ne sont pas nulles. C’est à dire que la dimension utile de $X$ est réduite à 60. La réduction de dimension va grandement simplifier notre calcul.
A là différence de Lasso, PCA n’utilise pas $Y$.

5. Suivant les observations de la question (Q4), appliquer la méthode de “PCA before OLS” qui consiste à appliquer OLS avec Y et XtrainV(1:60), où V(1:60) contient les vecteurs propres (associés aux 60 plus grandes valeurs propres) de la matrice de covariance. Faire une ré- gression linéaire (avec intercept), puis tracer les valeurs des coefficients (hors intercept). Sur un autre graphique, faire de même avec la méthode des moindres carrés classique.

u[:,4].shape

(210,)

# use PCA to select 60 features, we constructed 60 new features
Xpca = np.dot(Xtrain, u[:, :60])
np.shape(Xpca)

(353, 60)

# plot the Xpca features
XpcaDf=pd.DataFrame(Xpca)
ytrainDf=pd.DataFrame(ytrain)
Xypca = pd.concat([XpcaDf, ytrainDf], axis=1)
sns.pairplot(Xypca.iloc[:,0:5], diag_kind='kde')

//anaconda3/lib/python3.7/site-packages/statsmodels/nonparametric/kde.py:447: RuntimeWarning: invalid value encountered in greater
  X = X[np.logical_and(X > clip[0], X < clip[1])] # won't work for two columns.
//anaconda3/lib/python3.7/site-packages/statsmodels/nonparametric/kde.py:447: RuntimeWarning: invalid value encountered in less
  X = X[np.logical_and(X > clip[0], X < clip[1])] # won't work for two columns.

<seaborn.axisgrid.PairGrid at 0x1c23879e10>

png

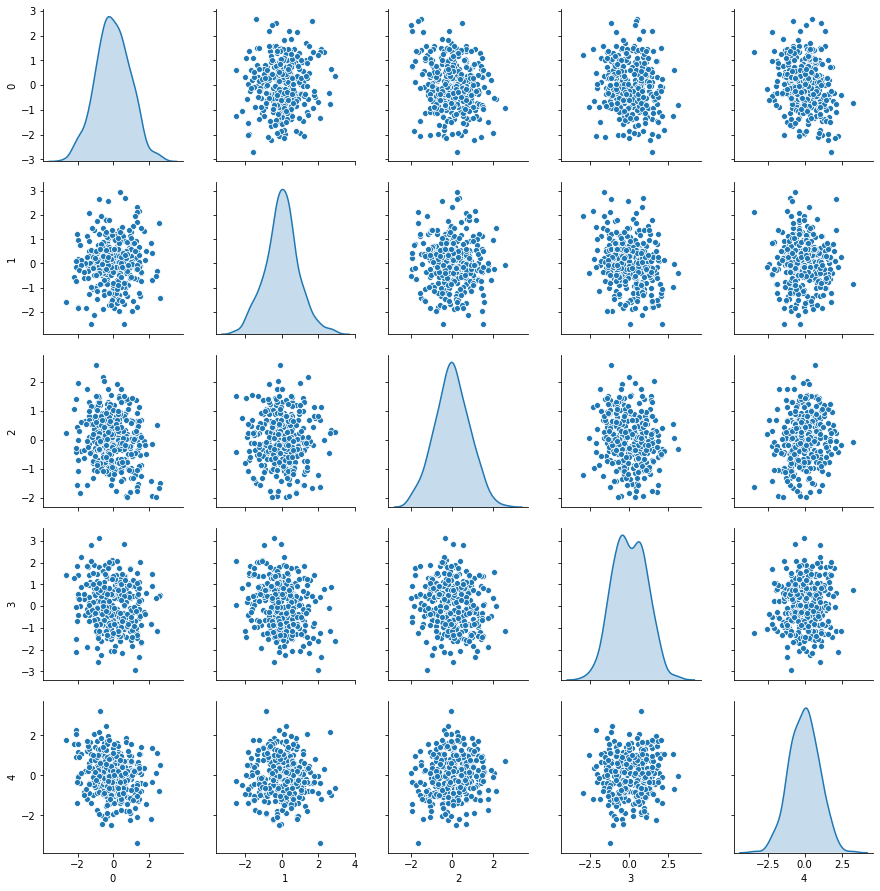
XpcaDf.corr().head()

	0	1	2	3	4	5	6	7	8	9	...	50	51	52	53	54	55	56	57	58	59
0	1.000000	0.085194	-0.183201	-0.098229	-0.235576	-0.152092	-0.017954	-0.140142	0.012558	0.183261	...	-0.132034	0.072273	-0.042997	-0.140756	-0.020877	-0.017995	0.030632	0.067088	0.039327	-0.063550
1	0.085194	1.000000	-0.031230	-0.227114	-0.045938	0.022046	-0.337616	-0.294434	-0.066662	-0.038033	...	0.168272	-0.100650	0.033290	-0.093838	-0.225531	0.023653	0.088042	-0.048892	-0.077742	0.039389
2	-0.183201	-0.031230	1.000000	-0.137852	0.128308	-0.098323	-0.071304	-0.163373	-0.071572	-0.076612	...	-0.094093	0.284289	-0.182953	0.031938	0.034216	0.077191	-0.045850	0.112738	-0.310940	-0.003263
3	-0.098229	-0.227114	-0.137852	1.000000	0.060702	-0.060384	0.042075	0.195657	0.183909	0.080632	...	-0.141497	-0.201097	0.108514	0.143150	-0.049108	-0.157196	-0.077540	-0.123943	-0.135105	-0.010146
4	-0.235576	-0.045938	0.128308	0.060702	1.000000	0.335518	0.003202	-0.136064	-0.089372	-0.093447	...	0.033285	0.040211	-0.108555	0.069908	-0.080901	0.069075	0.060297	0.193705	-0.123608	0.024527

5 rows × 60 columns

reg_pca = LinearRegression(fit_intercept=True).fit(Xpca,ytrain)
reg_pca.intercept_
reg_pca.coef_

array([  13.33696537,  104.99757657,  228.02354593,   20.16280823,
        -46.62608931,  147.97647321,   58.69720041,   51.80726   ,
         88.07394859,  103.39477962,   51.0513435 ,  -37.4326015 ,
         15.41295963,   15.03021349,  -92.58567489,   40.83679478,
        -46.11519151,  -52.56676589,  -57.70497346,   15.02738181,
         19.45308737,   37.47981208,  -41.2182203 ,   13.29180675,
         21.90546825,  -84.51614642,   65.33418478,   76.56174424,
         94.43034423,  -98.67594014,   14.55206168,   15.49197058,
        123.46727332,    9.28036132,   22.1893462 ,  -61.23698277,
          6.59869032, -132.72207723,   39.03882469,  103.57856351,
       -120.45299312,  -50.14481037,  -20.34188112,   18.60421744,
        115.64457525,   53.55207492,   14.62083924,  -43.45894277,
        -39.98910174,   20.71859287,  -38.10906733,   33.26906787,
        106.58800732,   98.50283596,   91.35817256,  -45.6098548 ,
         97.48920819,   23.85370504,   78.95919969, -182.75105545])

plt.scatter(range(reg_pca.coef_.shape[0]),reg_pca.coef_)

<matplotlib.collections.PathCollection at 0x1c2485af28>

png

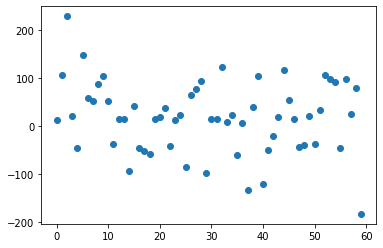
PCA a conçu 60 features qui contiennent maximum d’information avec une variance

reg = LinearRegression(fit_intercept=True).fit(Xtrain, ytrain)
reg.intercept_
reg.coef_

array([ 1.48086990e+15,  8.76297145e+14, -2.64089248e+15, -3.38106020e+15,
       -1.46472456e+15, -5.46096140e+14,  8.36579633e+14,  2.16351566e+15,
       -1.60489133e+15, -2.04791815e+15, -3.38925858e+14,  9.97287848e+14,
       -1.60589973e+15,  1.08509758e+15,  1.86837274e+15,  1.78112483e+15,
       -1.01249754e+15, -1.07982784e+15,  1.65532833e+15, -1.19552575e+15,
        9.30662518e+14,  2.22012678e+15,  1.09437136e+15,  5.50000000e+00,
       -1.75264612e+14, -4.91751919e+14,  1.62092131e+15,  7.12713199e+14,
        3.12107238e+14, -5.20201606e+14, -1.63583300e+15, -1.94992614e+15,
        6.21124410e+14,  4.31128731e+14,  1.80000000e+01,  1.83761308e+15,
        2.71410548e+15,  1.06195818e+15, -1.00964956e+15, -1.42329341e+15,
        1.86956169e+15,  9.65695708e+14,  2.93503913e+15, -2.57733692e+15,
        1.80562476e+15,  2.08233158e+15,  4.36326117e+15,  8.66728732e+14,
       -1.43185638e+15, -4.99868655e+14, -3.74467785e+15, -1.02074791e+15,
       -1.25359629e+15,  8.60253143e+14,  1.22753132e+15, -7.05875784e+14,
       -7.32329397e+14, -1.10418269e+15,  2.42812500e+01, -2.24705845e+15,
       -1.83909991e+14,  3.51818137e+15, -1.25528963e+15,  2.43318868e+15,
        4.17833499e+14,  4.15246423e+14,  1.91203785e+15, -3.85749679e+15,
        1.40019697e+15, -2.09241565e+15, -8.24580710e+14,  9.96475934e+14,
       -3.92292979e+14, -2.70630659e+15,  3.48468800e+14,  2.49295045e+15,
       -7.19174248e+14, -1.07756504e+15,  2.17738077e+14,  1.42500000e+01,
       -4.68111662e+14, -1.04376311e+15, -1.35979125e+15, -8.68290602e+14,
       -1.19837098e+15, -6.81233748e+14,  1.44758662e+14, -6.76382255e+14,
       -5.49775925e+14,  2.22977565e+15, -7.47753342e+14,  8.50899681e+14,
        2.85426104e+14, -7.26613728e+14, -1.26419367e+15, -2.25142303e+15,
        7.84968171e+14, -1.25855070e+15,  1.79563443e+15,  1.00000000e+00,
       -2.29183540e+15,  4.99537776e+14,  6.32240262e+14, -3.93757273e+14,
        3.68608983e+14, -1.26840928e+15,  1.70293826e+14, -1.82891835e+15,
        1.30568797e+15, -2.92961527e+15, -3.25208701e+14, -7.01164229e+14,
        4.33604063e+14, -4.37517578e+15,  1.46275138e+15,  3.11391127e+14,
       -5.34670643e+14, -4.06107885e+14, -2.97489522e+14,  6.76009172e+14,
       -1.39518795e+15,  1.93777719e+15, -2.90392864e+15,  3.21875000e+01,
       -2.93644102e+15,  1.48580537e+15, -2.63292378e+15,  2.81372182e+14,
       -2.16440308e+14,  2.12736429e+15,  5.38497733e+14,  1.24015069e+14,
       -1.54748675e+15, -3.00000000e+01, -1.82977434e+15, -1.11250000e+01,
        9.19695554e+13, -1.66382540e+15, -3.68371412e+15, -1.79084383e+15,
       -8.15060036e+14,  6.45915584e+13,  1.11694752e+15,  4.55563658e+14,
       -1.14414732e+15,  3.36687477e+14, -2.86680443e+15,  3.16070655e+15,
        7.71268722e+14,  2.69653269e+14,  2.68656379e+14, -9.56219990e+14,
        1.51097333e+15, -2.30060350e+15,  5.43460749e+14,  3.69202791e+14,
        9.43706022e+14,  8.28099910e+13,  1.14166846e+15,  1.28156247e+15,
        1.33050528e+15,  1.10497808e+15, -7.22906606e+14,  1.59133047e+15,
        3.72786194e+13,  3.61949753e+14, -1.04647788e+14,  1.40000000e+01,
        5.40701705e+13, -8.78254964e+14, -1.24407528e+15,  1.55967332e+13,
       -1.32383138e+15, -1.15107294e+15,  1.15000000e+01, -1.08921779e+12,
       -1.25575955e+15, -7.06282497e+14, -5.60639479e+14,  6.55070125e+14,
       -1.51271740e+14,  3.83167230e+14,  1.33131797e+15, -6.19030532e+14,
       -7.33467614e+13, -1.33939129e+14,  3.27491400e+14,  2.49139854e+14,
        1.70465492e+14,  6.12920332e+14,  7.32716795e+14,  2.02116580e+15,
        2.42460494e+15, -8.97896485e+14,  5.36692687e+14,  7.64003118e+14,
        1.83583576e+15,  1.58196014e+15,  4.70304062e+14,  5.23862565e+14,
        3.39942085e+13,  2.17158102e+14, -1.31245735e+15,  2.67483810e+15,
       -1.43985322e+15,  8.37318722e+14,  1.53536926e+15, -1.88287095e+15,
        1.48811774e+14, -7.95829555e+14])

reg_pca.coef_.shape[0]

plt.scatter(range(reg.coef_.shape[0]), reg.coef_)

<matplotlib.collections.PathCollection at 0x1c1fff5080>

png

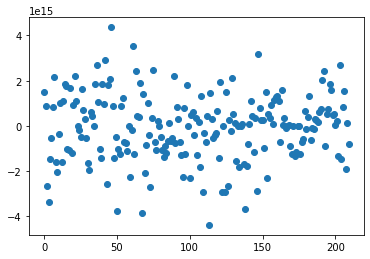
Sans PCA, on a beaucoup de bruit, le modele doit faire des coefficients très grandes à l’ordre de 10puissance 15 pour converger. Les coefficients estimés sont très erratiques, exagérément dépendants de l’échantillon d’apprentissage et pas du tout fiable pour la généralisation.

6. Donner les valeurs des intercepts pour les 2 régressions précédentes. Donner la valeur moyenne de la variable Y (sur le train set). Les intercepts des 2 questions sont-ils égaux ? Commenter. Uniquement pour cette question, centrer et réduire les variables après ACP (de petite dimension). Faire une régression avec ces variables et vérifier que l’intercept est bien égal à la moyenne de Y sut le train.

print('reg_pca.intercept_', reg_pca.intercept_)
print('reg.intercept_', reg.intercept_)
print('mean of Y', ytrain.mean())

Xpca_c = Xpca - Xpca.mean()
Xpca_cn = Xpca_c/np.sqrt(Xpca.var())

reg_pca.intercept_ 152.21888175345356
reg.intercept_ 151.74012924929178
mean of Y 150.97450424929178

reg6 = LinearRegression(fit_intercept=True).fit(Xpca_cn, ytrain)
print('intercept of Xpca centré réduit', reg6.intercept_)
print('mean of Y', ytrain.mean())

intercept of Xpca centré réduit 154.95153329388575
mean of Y 150.97450424929178

plt.scatter(range(reg6.coef_.shape[0]),reg6.coef_)

<matplotlib.collections.PathCollection at 0x1c24ccce80>

png

7. Pour les 2 méthodes (OLS et PCA before OLS) : Tracer les résidus de la prédiction sur l’échantillon test. Tracer leur densité (on pourra par exemple utiliser un histogramme). Calculer le coefficient de détermination sur l’échantillon test. Calculer le risque de prédiction sur l’échantillon test.

ytestOLS = reg.predict(Xtest)
ytestPCA = reg_pca.predict(np.dot(Xtest, u[:, :60]))

residusOLS = ytest - ytestOLS
residusPCA = ytest - ytestPCA

plt.subplot(121)
plt.scatter(range(len(residusOLS)), residusOLS)
plt.subplot(122)
plt.scatter(range(len(residusPCA)), residusPCA)

<matplotlib.collections.PathCollection at 0x1c326948d0>

png

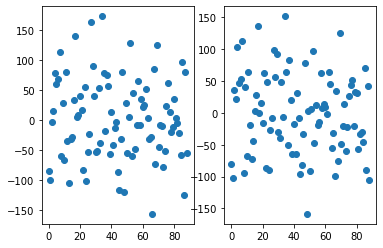
plt.subplot(121)
plt.hist(residusOLS)
plt.subplot(122)
plt.hist(residusPCA)

(array([ 1.,  3., 11., 11., 17., 14., 16.,  8.,  5.,  3.]),
 array([-158.48613422, -127.48582847,  -96.48552272,  -65.48521698,
         -34.48491123,   -3.48460548,   27.51570026,   58.51600601,
          89.51631176,  120.5166175 ,  151.51692325]),
 <a list of 10 Patch objects>)

png

plt.subplot(121)
sns.distplot(residusOLS, bins=20, kde=True)
plt.subplot(122)
sns.distplot(residusPCA, bins=20, kde=True)

<matplotlib.axes._subplots.AxesSubplot at 0x1c329269e8>

png

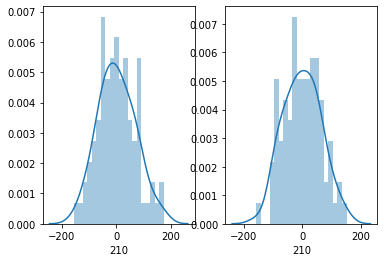
print("R2 for OLS          ", r2_score(ytest, reg.predict(Xtest)))
print("R2 for OLS with PCA:", r2_score(
    ytest, reg_pca.predict(np.dot(Xtest, u[:, :60]))))

R2 for OLS           0.31091177660371383
R2 for OLS with PCA: 0.4037591017028014

print("prediction risk = MSE for OLS         ",
      mean_squared_error(ytest, reg.predict(Xtest)))
print("prediction risk = MSE for OLS with PCA:", mean_squared_error(
    ytest, reg_pca.predict(np.dot(Xtest, u[:, :60]))))

prediction risk = MSE for OLS          4574.783378254781
prediction risk = MSE for OLS with PCA: 3958.379868287305

Coder la méthode de forward variable sélection. On pourra utiliser la statistique du test de nullité du coefficient (comme vu en cours). Pour l’instant, on ne met pas de critère d’arret sur la méthode. C’est à dire que l’on ajoute une variable à chaque étape jusqu’à retrouver la totalité des variables. Afficher l’ordre de séléction des variables.

def forward_variable_selection(Xtrain, ytrain):

    features_selected = {}
    features_list = list(range(0, len(Xtrain.columns)))
    t_stat_max = 0

    p_values_selected = {}

    t_stat_history = []
    stop_index = []

    while len(features_list) > 0:
        # Number of samples, t_stat and residual
        t_stat = []
        y_res = []
        n = len(ytrain)

        # for each xi
        for i in features_list:

            # lineair regression on feature xi
            modelxi = LinearRegression(fit_intercept=True)
            modelxi.fit(Xtrain[[i]], ytrain)
            y_predxi = modelxi.predict(Xtrain[[i]])

            # Variance of y et variance of theta
            # formule referred to https://stattrek.com/regression/slope-test.aspx
            sigma_res = ((ytrain - y_predxi)**2).sum()/(n-2)
            sigma_coef = np.sqrt(
                sigma_res / ((Xtrain[i] - Xtrain[i].mean())**2).sum())

            # T statistcs
            statistique = float(abs(modelxi.coef_/sigma_coef))

            # record all the residus and T statistique
            y_res.append(ytrain - y_predxi)
            t_stat.append(statistique)
            t_stat_history.append(statistique)

        # select the feature with the max t_stat
        t_stat_max = max(t_stat)
        ind_max = t_stat.index(t_stat_max)

        # Record everytime the selected features
        features_selected[features_list[ind_max]] = t_stat_max

        # calculate p value for the feature with max t_stat
        # A Student’s distribution , n-2 is the degree of freedom
        # cdf : Cumulative distribution function.
        p_value_max = (1 - stat.t.cdf(abs(t_stat_max), n - 2)) * 2

        # Record pvalue for all the selected features
        p_values_selected[features_list[ind_max]] = p_value_max

        # Y updated: y minus the impact of the chosen Xi on y
        ytrain = y_res[ind_max]

        # delete from features the Xi selected
        del features_list[ind_max]
        # end of the loop

    print("Liste features slected and their T-stat : ")
    print({k: features_selected[k] for k in list(features_selected)})

    return features_selected, p_values_selected, t_stat_history

features_selected8,p_values_selected8,t_stat_history8 = forward_variable_selection(Xtrain, ytrain)

Liste features slected and their T-stat : 
{123: 14.040272094250644, 58: 6.897141941360045, 133: 3.1833389751878807, 167: 4.040340152862388, 129: 2.6554566789514498, 49: 2.7141810970908224, 135: 2.3924398621698977, 93: 2.4260739497922152, 154: 2.1149719891804444, 26: 2.1046826755474926, 112: 1.8881083260562272, 51: 1.6678171499269927, 173: 1.7761812802663048, 132: 1.6381676486489087, 96: 1.4707157985885062, 171: 1.2191989252847166, 64: 1.2346623209206617, 38: 1.1999816034062323, 27: 1.003651322375976, 110: 1.0859616050375411, 206: 0.8820396012875202, 130: 0.8809392190201433, 14: 0.7976459015746905, 79: 0.7742272093529635, 162: 0.7637861986452845, 28: 0.8689947251144713, 99: 0.7797500111209399, 61: 0.7158113791437613, 144: 0.7233905562978864, 182: 0.6736636693375975, 168: 0.5861267607386345, 208: 0.606864040592687, 175: 0.5748344754065808, 158: 0.541286702423264, 119: 0.5323965575917982, 181: 0.5130803301886856, 140: 0.5137099854023118, 202: 0.4331897691055989, 174: 0.41195241707929287, 145: 0.4183220875291923, 7: 0.37639859994234165, 86: 0.32369508387907175, 92: 0.3007369689176699, 148: 0.3288393843476035, 68: 0.28079267228185356, 21: 0.29525466521533644, 15: 0.23047428031180647, 160: 0.25792798785727866, 16: 0.21211448167848462, 114: 0.2027375048280936, 137: 0.21168918037432088, 94: 0.18584684703860374, 1: 0.17844332402132118, 138: 0.16898397283084765, 8: 0.15621696168815966, 187: 0.14489850495524015, 18: 0.13451281415880004, 176: 0.13964170921470218, 204: 0.12912350449221943, 100: 0.12083882274376796, 0: 0.11696463688264785, 164: 0.11888866783142871, 60: 0.10930613339391602, 170: 0.12156622610612774, 149: 0.11516425544361712, 98: 0.10555829323638381, 128: 0.09968929610230604, 142: 0.10293478961128125, 185: 0.09218794874973359, 74: 0.09188451403727743, 31: 0.09092836229259989, 23: 0.09509560653334283, 2: 0.07309991638988879, 186: 0.06711234409235253, 203: 0.07093676725163134, 209: 0.07413496970119157, 157: 0.05335353542256872, 141: 0.055081541783946156, 40: 0.05428233646263387, 81: 0.04850393486061552, 44: 0.04604179302228368, 179: 0.046609295157431584, 198: 0.05049488724897866, 65: 0.04395272695827559, 95: 0.0429926124163935, 180: 0.04593003929941875, 143: 0.03918883496892082, 34: 0.03961526896607647, 151: 0.03579810347536384, 106: 0.03408418581223517, 36: 0.0353738741675707, 193: 0.041173562379924034, 9: 0.03008013165506461, 104: 0.029727085059316163, 33: 0.029954803728363986, 169: 0.028811557643301886, 196: 0.026460741078201306, 20: 0.027586608282699803, 188: 0.02816607675429368, 117: 0.021262211091056613, 72: 0.020743738516377983, 30: 0.020627169184833097, 75: 0.02189335300538528, 178: 0.019236253116647697, 70: 0.018516429109729726, 29: 0.015503701277166168, 5: 0.015178467197641229, 25: 0.014402436449096598, 116: 0.01807931082134749, 22: 0.014303675973176801, 67: 0.011547366216102199, 207: 0.011543343728675748, 155: 0.011252271463976175, 50: 0.013628865997317758, 102: 0.012445347474623074, 78: 0.01003180347512531, 126: 0.01105723675990212, 76: 0.0090833106520947, 199: 0.010075266657096961, 13: 0.007726655380706364, 88: 0.007648488988491812, 184: 0.007673291589914264, 97: 0.007663714321395779, 127: 0.006602402065919301, 118: 0.00622085283362835, 150: 0.005999459277399956, 139: 0.0060327189829646214, 201: 0.006151983950046631, 192: 0.005730896194994717, 6: 0.006172915070426707, 101: 0.006400245781291008, 84: 0.005891529626416971, 19: 0.00491805235881799, 91: 0.004424156686502118, 41: 0.004486494454641262, 39: 0.0044442118619661, 190: 0.004796670771262893, 55: 0.0039051973824439025, 183: 0.003662916887695215, 147: 0.0033577781692421898, 24: 0.0037743297160061054, 153: 0.0031679915158561982, 191: 0.0035077706663373225, 42: 0.0031808538855661976, 161: 0.003479237512461385, 59: 0.0029547337813701593, 122: 0.0031383973488147807, 194: 0.003212195674178396, 134: 0.0032828436284637213, 80: 0.002853477844563082, 54: 0.0032842987370358383, 121: 0.0024819063954913674, 57: 0.0022423843905814097, 146: 0.0025849108513157273, 3: 0.0021930386929279633, 107: 0.0020127502099650967, 10: 0.0018843045633499833, 197: 0.0018457766036199387, 17: 0.001956090443995008, 165: 0.00200966669022749, 82: 0.002043076727630592, 113: 0.002005661078445857, 90: 0.0017098890056445506, 109: 0.0016067736105263202, 200: 0.001877830401010328, 89: 0.0013800709059912854, 124: 0.0016092313346440592, 111: 0.0015869659970369505, 32: 0.0015179566841672604, 131: 0.001400364056118501, 63: 0.0013719458523484282, 85: 0.0013604799019305226, 45: 0.0014463963960225415, 56: 0.0013917326705246932, 12: 0.0010979477925341114, 177: 0.0011467761972698918, 156: 0.0012657882977796834, 172: 0.001260127565689647, 11: 0.0013724461775458377, 163: 0.0012716565060041432, 115: 0.001108766738616829, 105: 0.0008366799671030879, 43: 0.0007513368098121038, 47: 0.0008702323839303554, 69: 0.001070076681847302, 103: 0.0008921908651520029, 120: 0.0008387682503530396, 71: 0.0006530850656221169, 152: 0.0005563866969813374, 48: 0.0005734288396196621, 77: 0.0005057575691326309, 35: 0.0005033074031400605, 125: 0.0004378472844224013, 62: 0.00035650321000756216, 87: 0.0003978376888245606, 159: 0.0004122095514434207, 66: 0.000340251392238214, 189: 0.00033920342339637904, 166: 0.0003079858763384643, 136: 0.00026344933184881846, 108: 0.00030474705364991813, 195: 0.0002413167335475709, 52: 0.00018323162899308739, 4: 0.00018257570373570714, 53: 0.00017406190667692553, 205: 0.00012758174419884644, 37: 0.00012109109949931037, 73: 5.095502136370109e-05, 83: 3.1439869790582896e-05, 46: 4.348239387958716e-06}

Critère d’arrêt : On décide d’arrêter lorsque la p-valeur dépasse 0.1. Illustrer la méthode en donnant (i) les 3 graphes des statistiques obtenues lors de la sélection de la 1er, 2eme et 3eme variables (en abscisse : l’index des variables, en ordonné : la valeur des stats) , (ii) le graphe des 50 premières p-valeurs (dont chacune est associée à la variable sélectionnée). Sur ce même graphe, on tracera la ligne horizontale d’ordonnée 0.1. Enfin on donnera la liste des variables sélectionnées.

def forward_variable_selection_withThreshold(Xtrain, ytrain, p_value_threshold, nb_to_plot):
    features_list = list(range(0, len(Xtrain.columns)))

    features_selected = {}

    p_values_selected = {}

    p_value_max = 0

    t_stat_history = []
    stop_index = []
    j = 0

    while len(features_list) > 0 and p_value_max <= p_value_threshold:
        # Number of samples, t_stat and residual
        t_stat = []
        y_res = []
        n = len(ytrain)

        # for each xi
        for i in features_list:

            # lineair regression on feature xi
            modelxi = LinearRegression(fit_intercept=True)
            modelxi.fit(Xtrain[[i]], ytrain)
            y_predxi = modelxi.predict(Xtrain[[i]])

            # Variance of y et variance of theta
            # formule referred to https://stattrek.com/regression/slope-test.aspx
            sigma_res = ((ytrain - y_predxi)**2).sum()/(n-2)
            sigma_coef = np.sqrt(
                sigma_res / ((Xtrain[i] - Xtrain[i].mean())**2).sum())

            # T statistcs
            statistique = float(abs(modelxi.coef_/sigma_coef))

            # record all the residus and T statistique
            y_res.append(ytrain - y_predxi)
            t_stat.append(statistique)
            t_stat_history.append(statistique)

        # select the feature with the max t_stat
        t_stat_max = max(t_stat)
        ind_max = t_stat.index(t_stat_max)

        # calculate p value for the feature with max t_stat
        # A Student’s distribution , n-2 is the degree of freedom
        # cdf : Cumulative distribution function.
        p_value_max = (1 - stat.t.cdf(abs(t_stat_max), n - 2)) * 2

        # stop if p-value > threshold
        # print(break_point)
        if p_value_max > p_value_threshold:
           # break
            stop_index.append(j)

        j = j+1

        # Record pvalue for all the selected features
        p_values_selected[features_list[ind_max]] = p_value_max

        # Record everytime the selected features
        features_selected[features_list[ind_max]] = t_stat_max

        # Y updated: y minus the impact of the chosen Xi on y
        ytrain = y_res[ind_max]

        # delete from features the Xi selected
        del features_list[ind_max]
        # end of the loop

    print("Liste features slected and their T-stat : ")
    print({k: features_selected[k]
           for k in list(features_selected)[:min(stop_index)]})

    return features_selected, p_values_selected, t_stat_history

features_selected9, p_values_selected9, t_stat_history9 = forward_variable_selection_withThreshold(Xtrain, ytrain, 0.1, 50)

Liste features slected and their T-stat : 
{123: 14.040272094250644, 58: 6.897141941360045, 133: 3.1833389751878807, 167: 4.040340152862388, 129: 2.6554566789514498, 49: 2.7141810970908224, 135: 2.3924398621698977, 93: 2.4260739497922152, 154: 2.1149719891804444, 26: 2.1046826755474926, 112: 1.8881083260562272, 51: 1.6678171499269927, 173: 1.7761812802663048}

# T-Stat for the first round of selection
fig = plt.figure(figsize=(16, 3))
plt.plot(t_stat_history9[0:len(Xtrain.columns)-1],)

[<matplotlib.lines.Line2D at 0x1c32c57dd8>]

png

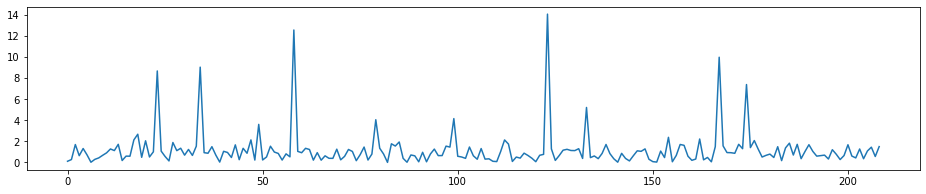
# T-Stat for the seconde round, we can see the highest peak in the first round has disappered
fig = plt.figure(figsize=(16, 3))
plt.plot(t_stat_history9[len(Xtrain.columns):2*len(Xtrain.columns)-1])

[<matplotlib.lines.Line2D at 0x1c32cf3898>]

png

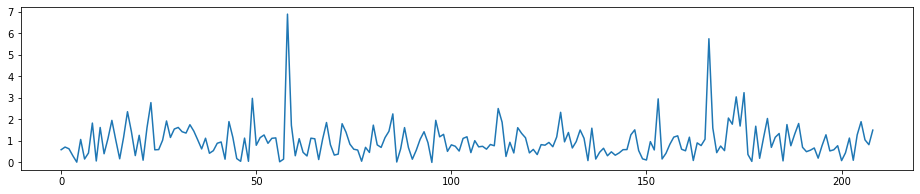
T-Stat for the seconde round, we can see the highest peak in the first round has disappered

# T-Stat for the 3rd round, we can see the highest peak in the 2nd round has disappered
fig = plt.figure(figsize=(16, 3))
plt.plot(t_stat_history9[len(Xtrain.columns)*2:3*len(Xtrain.columns)-1])

[<matplotlib.lines.Line2D at 0x1c32d52240>]

png

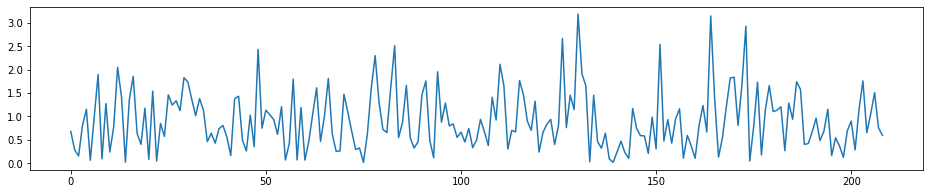
we can see the highest peak in the 2nd round has disappered, and after 2 features selected, the rest of the features left have smaller T-stat and are more homogenes.

# since in question 9 we just selected 8 features, I will use Q8 to show the 50 p values
fig = plt.figure(figsize=(10, 8))
plist = p_values_selected8.items()
k, v = zip(*plist)
plt.plot(v[0:50])
plt.axhline(y=0.1, color='g', linestyle='-')

<matplotlib.lines.Line2D at 0x1c32e716a0>

png

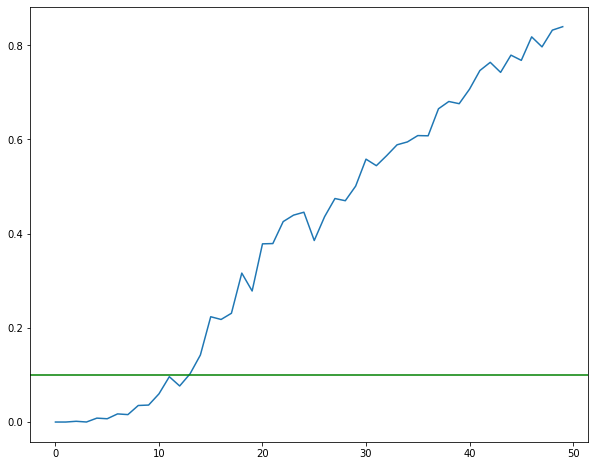
With threshold pvalue = 0.1, the Forward selected 14 features, the number varies each time, but always around 10. The value is not always ascending, this is normal, because each step we recalcul all.

# Feature Num : T stat
print("Feature Num : T stat")
features_selected9

Feature Num : T stat





{123: 14.040272094250644,
6.897141941360045,
3.1833389751878807,
4.040340152862388,
2.6554566789514498,
2.7141810970908224,
2.3924398621698977,
2.4260739497922152,
2.1149719891804444,
2.1046826755474926,
1.8881083260562272,
1.6678171499269927,
1.7761812802663048,
1.6381676486489087}

Appliquer OLS sur les variables sélectionnées. Donner le risque de prédiction obtenu l’échantillon test et le comparer à ceux de OLS et PCA before OLS.

# select the col
plist = features_selected9.items()
forward_col, v = zip(*plist)
forward_col = np.array(forward_col)

# Fit with LinearRegression and then predit
X_Forward = (Xtrain[forward_col])
regWithSFS = LinearRegression(fit_intercept=True).fit(X_Forward, ytrain)
ytestSFS = regWithSFS.predict(Xtest[forward_col])

# show the model params
print(regWithSFS.intercept_)
print(regWithSFS.coef_)

152.71611757714206
[34.24494572 21.54996471 -7.32701206 15.77779481 -7.79896878 -9.53781514
 -5.86406618  5.74650896 -6.02767736 -5.48874059  7.55992583 -5.81742285
 -4.49260448 -5.12974468]

print("prediction risk of OLS on Forword selected features is : ",
      mean_squared_error(ytest, regWithSFS.predict(Xtest[forward_col])))

print("R2 score of OLS on Forward selected features is :",
      r2_score(ytest, regWithSFS.predict(Xtest[forward_col])))

prediction risk of OLS on Forword selected features is :  3973.673571647234
R2 score of OLS on Forward selected features is : 0.4014554492659369

The score of OLS Forward is better than OLS and worse than PCA_OLS.

Afin de préparer la validation croisée, séparer l’échantillon train en 4 parties (appelées ”folds”) de façon aléatoire. On affichera les numéros d’échantillon sélectionnés dans chaque fold.

from sklearn.model_selection import KFold

kf = KFold(n_splits=4)
kf.get_n_splits(Xtrain)

print(kf)

KFold(n_splits=4, random_state=None, shuffle=False)

kf

KFold(n_splits=4, random_state=None, shuffle=False)

from sklearn.model_selection import KFold

kf = KFold(n_splits=4, shuffle=True, random_state=1)
kf.get_n_splits(Xtrain)

print(kf)

kf = kf.split(Xtrain)
folds = []
i = 1


for train_index, test_index in kf:
    folds.append([train_index, test_index])
    print(" Fold ", i, ":")
    print("Train : ", train_index)
    print(" ### ")
    print("Test : ", test_index)
    print(" ############ ")
    i = i+1

KFold(n_splits=4, random_state=1, shuffle=True)
 Fold  1 :
Train :  [  0   1   2   3   7   8   9  10  13  15  16  17  19  20  21  22  23  24
26  28  30  31  32  33  34  35  36  37  38  39  40  41  42  43  44
46  47  48  49  50  51  52  53  54  55  56  57  60  61  62  63  64
68  69  70  71  72  74  75  76  77  78  79  81  82  83  84  86  87
94  96  97  98  99 100 101 103 104 108 109 110 113 114 115 116 117
121 123 124 126 128 129 130 132 133 134 135 136 137 138 139 140 141
143 144 145 146 147 148 149 151 152 153 155 156 157 159 160 161 162
166 168 170 172 175 176 177 178 179 181 182 183 184 187 189 190 191
193 194 195 196 197 198 200 202 203 205 206 207 208 209 210 212 213
215 216 220 221 222 225 226 228 229 230 231 233 234 235 237 239 240
243 244 245 246 248 250 251 252 253 254 255 256 258 259 261 262 263
265 266 267 269 273 276 277 278 279 280 281 282 283 284 285 287 288
290 291 292 293 296 297 301 302 304 305 306 307 309 310 311 313 315
317 318 319 320 321 322 323 325 326 327 328 330 331 332 333 334 335
338 339 340 341 342 343 345 346 347 348 351]
 ### 
Test :  [  4   5   6  11  12  14  18  27  29  58  59  65  67  73  80  85  89  90
92  93  95 102 105 106 107 111 112 119 120 122 125 127 131 150 154
163 165 167 169 171 173 174 180 185 186 188 199 201 204 211 217 218
223 224 227 232 236 238 242 247 249 257 260 268 270 271 272 274 275
294 295 298 299 300 303 308 312 314 324 329 337 344 349 350 352]
 ############ 
 Fold  2 :
Train :  [  1   2   3   4   5   6   7  10  11  12  13  14  15  18  20  21  22  23
25  26  27  29  30  36  37  40  43  45  47  49  50  52  53  54  56
58  59  60  61  64  65  67  68  69  71  72  73  74  75  76  77  80
82  83  84  85  86  87  89  90  91  92  93  94  95  96  97  98 101
103 104 105 106 107 109 111 112 113 114 115 116 118 119 120 121 122
125 126 127 129 130 131 133 134 135 136 137 140 141 142 143 144 145
149 150 151 152 153 154 155 156 158 160 163 164 165 166 167 168 169
171 173 174 176 177 178 180 181 182 183 184 185 186 187 188 190 193
195 196 198 199 200 201 202 203 204 206 209 210 211 212 214 215 216
218 219 220 222 223 224 226 227 228 230 232 233 235 236 237 238 239
241 242 243 246 247 248 249 252 253 254 255 256 257 259 260 262 263
265 266 267 268 269 270 271 272 273 274 275 276 279 280 281 282 283
286 287 288 293 294 295 297 298 299 300 302 303 305 306 308 309 310
313 314 315 316 317 318 319 320 323 324 325 326 327 328 329 330 335
338 339 341 342 343 344 347 348 349 350 351 352]
 ### 
Test :  [  0   8   9  16  17  19  28  31  32  33  34  35  38  39  41  42  44  46
51  55  62  63  66  70  78  79  88  99 100 108 110 117 123 128 132
139 146 147 157 159 161 162 172 175 179 189 191 192 197 205 207 208
221 225 229 231 234 244 245 250 251 258 261 277 278 284 289 290 291
296 301 304 307 311 321 322 331 332 333 334 336 340 345 346]
 ############ 
 Fold  3 :
Train :  [  0   1   2   3   4   5   6   7   8   9  11  12  14  15  16  17  18  19
25  26  27  28  29  30  31  32  33  34  35  37  38  39  41  42  43
46  48  49  50  51  52  55  58  59  62  63  64  65  66  67  68  70
72  73  74  76  77  78  79  80  83  85  86  87  88  89  90  91  92
95  99 100 102 104 105 106 107 108 109 110 111 112 115 117 119 120
122 123 125 126 127 128 129 131 132 133 136 138 139 141 143 144 146
149 150 151 153 154 155 156 157 158 159 161 162 163 165 166 167 169
172 173 174 175 178 179 180 183 185 186 188 189 190 191 192 195 196
199 200 201 203 204 205 207 208 209 211 213 215 216 217 218 219 221
224 225 226 227 229 231 232 234 235 236 237 238 239 241 242 243 244
247 249 250 251 252 253 254 255 257 258 259 260 261 262 263 264 265
268 270 271 272 274 275 276 277 278 279 280 281 282 284 286 288 289
291 292 293 294 295 296 297 298 299 300 301 303 304 307 308 309 311
313 314 316 317 319 320 321 322 324 325 326 329 330 331 332 333 334
336 337 340 341 343 344 345 346 348 349 350 352]
 ### 
Test :  [ 10  13  20  21  23  24  36  40  45  47  53  54  56  57  60  61  69  75
82  84  94  96  97  98 101 103 113 114 116 118 124 130 134 135 137
142 145 148 152 160 164 168 170 176 177 181 182 184 187 193 194 198
206 210 212 214 220 222 228 230 233 240 246 248 256 267 269 273 283
287 302 305 306 310 315 318 323 327 328 338 339 342 347 351]
 ############ 
 Fold  4 :
Train :  [  0   4   5   6   8   9  10  11  12  13  14  16  17  18  19  20  21  23
27  28  29  31  32  33  34  35  36  38  39  40  41  42  44  45  46
48  51  53  54  55  56  57  58  59  60  61  62  63  65  66  67  69
73  75  78  79  80  81  82  84  85  88  89  90  91  92  93  94  95
97  98  99 100 101 102 103 105 106 107 108 110 111 112 113 114 116
118 119 120 122 123 124 125 127 128 130 131 132 134 135 137 138 139
142 145 146 147 148 150 152 154 157 158 159 160 161 162 163 164 165
168 169 170 171 172 173 174 175 176 177 179 180 181 182 184 185 186
188 189 191 192 193 194 197 198 199 201 202 204 205 206 207 208 210
212 213 214 217 218 219 220 221 222 223 224 225 227 228 229 230 231
233 234 236 238 240 242 244 245 246 247 248 249 250 251 256 257 258
261 267 268 269 270 271 272 273 274 275 277 278 283 284 285 286 287
290 291 292 294 295 296 298 299 300 301 302 303 304 305 306 307 308
311 312 314 315 318 321 322 323 324 327 328 329 331 332 333 334 336
338 339 340 342 344 345 346 347 349 350 351 352]
 ### 
Test :  [  1   2   3   7  15  22  25  26  30  37  43  49  50  52  64  68  71  72
76  77  83  86  87 104 109 115 121 126 129 133 136 141 143 144 149
153 155 156 166 178 183 190 195 196 200 203 209 215 216 226 235 237
241 243 252 253 254 255 259 262 263 264 265 266 276 279 280 281 282
293 297 309 313 316 317 319 320 325 326 330 335 341 343 348]
 ############ 

print("K folds,K-1 in train and 1 in test(1/K) ")
print(len(test_index))
len(train_index)

K folds,K-1 in train and 1 in test(1/K) 
88

265

Appliquer la méthode de la régression ridge. Pour le choix du paramètre de régularisation, on fera une validation croisée sur les ”folds” définies lors de la question précédente. A tour de rôle chacune des ”folds” servira pour calculer le risque de prédiction alors que les autres seront utilisées pour estimer le modèle. On moyennera ensuite les 4 risques de prédictions. On donnera la courbe du risque de validation croisée en fonction du paramètre de régularisation (on veillera à bien choisir l’espace de définition pour le graphe). Donner le paramètre de régularisation optimal et la valeur du risque sur le test.

Minimizes the objective function:

y - Xw

^2_2 + alpha *

^2_2

from sklearn.linear_model import Ridge
import statistics

# List of alphas
alphas_list = np.linspace(0.001, 200, 200)

# to record prediction risk CV
R_pred_cv = []
coefs = []

# Cross Validation to find best regulation parameter
for alpha_i in alphas_list:

    # Initiliazation de la liste des risque de predictions pour chacun des k-folds
    R_pred = []
    i = 1
    # Regression Ridge sur les CV 4 folds, we do 4 times CV and train 4 times Ridge model
    for train_index, validation_index in folds:
        # Train Ridget model, CV=4
        # Regression Ridge: need to do recentrage before training :  fit_intercept=True
        ridge = Ridge(alpha=alpha_i, fit_intercept=True, max_iter=None,
                      normalize=False, random_state=None,
                      solver='auto', tol=0.001).fit(Xtrain.iloc[train_index], ytrain.iloc[train_index])
        # Prediction
        Y_pred = ridge.predict(Xtrain.iloc[validation_index])

        # treatment
        # record prediction risk
        p_r = mean_squared_error(ytrain.iloc[validation_index], Y_pred)
        R_pred.append(p_r)

        # chose the coef for the best ridgt model
        best_ridgt_coef = ridge.coef_
        if (i == 1):
            best_ridgt_coef = ridge.coef_
        if (i != 1 and R_pred[-1] < R_pred[-2]):
            best_ridgt_coef = ridge.coef_
        i = i+1

    # calcul the mean of prediction risk of ridge on 4 cross validation
    R_pred_cv_mean = np.mean(R_pred)
    R_pred_cv.append(R_pred_cv_mean)
    # record the best
    coefs.append(best_ridgt_coef)

# chose the smallest alpha
ind_min = R_pred_cv.index(min(R_pred_cv))
alpha_opt = alphas_list[ind_min]

fig = plt.figure()
fig.suptitle(
    'Cross-Validation du Paramètre de régularisation Ridge', fontsize=16)
plt.plot(alphas_list, R_pred_cv)
plt.axvline(alpha_opt, color='g',)
plt.xlabel(r'$\alpha$')
plt.ylabel('Score')
plt.show()

print("The best regulation hyperparameter of RIDGE trained by cross Validation is : ", alpha_opt)

png

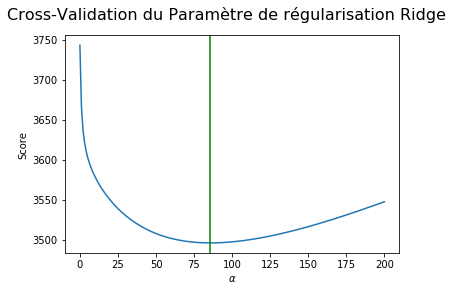
The best regulation hyperparameter of RIDGE trained by cross Validation is :  85.42770854271357

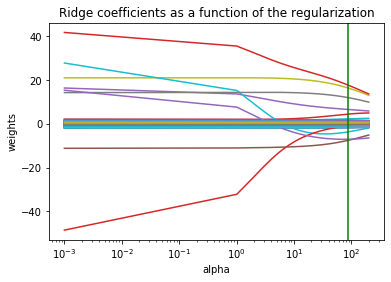
ax = plt.gca()
ax.plot(alphas_list, coefs)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1])  # reverse axis
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('Ridge coefficients as a function of the regularization')
plt.axvline(alpha_opt, color='g',)
plt.axis('tight')
plt.show()

png

A l’aide de la fonction lassoCV de sklearn, choisir le paramètre de régularisation du LASSO. Donner le risque de prédiction associé.

# CV train Lasso
lasso_model_cv = LassoCV(alphas=np.linspace(1,1000, 4000),cv=4,fit_intercept=True)
lasso_model_cv.fit(Xtrain, ytrain)

#prediction
Y_pred_lasso = lasso_model_cv.predict(Xtest)
R_pred_lasso = mean_squared_error(ytest, Y_pred_lasso)

print("Alpha chosen ", lasso_model_cv.alpha_)
print("Risque de prediction lasso: ", R_pred_lasso)

Alpha chosen  3.7479369842460617
Risque de prediction lasso:  3695.826175907521

Donner les variables selectionées par le lasso. Combien y-en a t-il ? Appliquer la méthode OLS aux variables sélectionnées. Cette méthode est appelé Least-square LASSO.

np.count_nonzero(lasso_model_cv.coef_)

i = -1
lasso_cols = []
for c in lasso_model_cv.coef_:
    i = i+1
    if c != 0:
        lasso_cols.append(i)
        print(i, c)

0.42499535042069947
-0.2370167834148353
0.23136752826972223
1.170730703991482
-0.23810042819357274
-0.8366201767243908
-3.752636561068908
18.8806600437205
-3.6426587626988765
-0.7900200300401119
1.6277903488099912
1.4395051136918504
0.32010081186271344
0.4863435688297971
25.50141744065234
-3.5476916464481936
-1.2178045899072705
-3.631652202151391
-1.9825679547672914
13.11723558532276
-0.289561117541825
-5.914731797442394
0.4711019613390468
-0.3379602119996976

lasso_cols = [i for i, c in enumerate(lasso_model_cv.coef_) if c]
print("The best Lasso Lambda chosen is ", lasso_model_cv.alpha_)
print("the selected features :", lasso_cols)

The best Lasso Lambda chosen is  3.498749374687344
the selected features : [13, 17, 20, 23, 26, 31, 49, 58, 85, 88, 93, 112, 113, 117, 123, 129, 132, 135, 154, 167, 172, 174, 176, 209]

# OLS LASSO CV model
XlassoCV = (Xtrain[lasso_cols])
regWithLasso = LinearRegression(fit_intercept=True).fit(XlassoCV, ytrain)

# show the OLS lasso result
print(regWithLasso.intercept_)
print(regWithLasso.coef_)

# Prediction
ytestLassoCV = regWithLasso.predict(Xtest[lasso_cols])

152.73672947088406
[ 1.03552816 -0.20532299 -0.57026317  3.86871148 -3.58291099 -5.13667258
 -5.4539995  19.06528571 -7.7255759  -3.97591715  5.64194945  2.88542817
  0.99010539  3.05170391 26.67884882 -6.83795429 -4.75730245 -8.26380768
 -2.30877105 15.34862114 -2.97791013 -9.31653777  2.31939002 -1.61850549]

print("prediction risk of OLS on Lasso selected features is : ",
      mean_squared_error(ytest, regWithLasso.predict(Xtest[lasso_cols])))

print("R2 score of OLS on Lasso selected features is :", r2_score(
    ytest, regWithLasso.predict(Xtest[lasso_cols])))

prediction risk of OLS on Lasso selected features is :  3829.817005946787
R2 score of OLS on Lasso selected features is : 0.4231242053765768

Cette dernière question est un question d’ouverture vers une approche non-linéaire. En utilisant les variables séléctionées par le LASSO (Q13) ou par la méthode forward (Q9), mettre au point une méthode de regression non-linéaire. On apprendra les différents paramètres par validation croisée et l’on donnera la valeur du risque de prédiction calculé sur l’échantillon test. Des performances moindres par rapport à OLS peuvent se produire. Commenter.

On teste d’abord un modèle pomynomial. Mais clairement le modèle polynomial est overfitted.

# Firstly we will test PolynomialFeatures
from sklearn.preprocessing import PolynomialFeatures

poly = PolynomialFeatures(2, interaction_only=True)
XtrainNonLinear = poly.fit_transform(Xtrain[lasso_cols])
Xpoly= poly.fit(Xtrain[lasso_cols])
XtestNonLinear = poly.transform(Xtest[lasso_cols])

reg15 = LinearRegression(fit_intercept=True).fit(XtrainNonLinear, ytrain)

print("prediction risk is : ",
      mean_squared_error(ytest, reg15.predict(XtestNonLinear)))

print("R2 score  :", r2_score(
    ytest, reg15.predict(XtestNonLinear)))

prediction risk is :  16960.864449702003
R2 score  : -1.5547727585232725

On teste ensuite un autre modèle non linéaire: Random Forest

from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import cross_val_score

# score of the CV of RandomForest
scores = cross_val_score(regRandomForest, Xtrain, ytrain,
                         scoring="neg_mean_squared_error", cv=5)

MSE_CV = - scores
print("prediction risk of Random Forest on each Cross Validation ", MSE_CV)
# calcul the écart type of the cross validation
print("standard error of MSE Cross validation :", np.std(MSE_CV))

print("prediction risk of cross validation", MSE_CV.mean())
print("R2 score of RF on Lasso selected features is :", r2_score(
    ytest, regRandomForest.predict(Xtest[lasso_cols])))

prediction risk of Random Forest on each Cross Validation  [4022.56710896 2789.49202006 3380.66456194 3565.80554527 4520.63505802]
standard error of MSE Cross validation : 585.9600347573994
prediction risk of cross validation 3655.8328588495397
R2 score of RF on Lasso selected features is : 0.40190418470553135

Etape CV : Durant la validation croisée, on voit que le modele Random Forest est rélativement stable (écart type).

Pour simplifier, on utilise GridSearchCV pour trouver les meilleurs parametres en utilisant validation croisée.

from sklearn.model_selection import GridSearchCV

#We do a cross validation on training dataset
param_grid = [{'max_depth': [1, 2, 3, 4,5],
               'max_features':[2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]}]

forest_reg = RandomForestRegressor()

grid_search = GridSearchCV(forest_reg, param_grid,
                           cv=4, scoring="neg_mean_squared_error")

grid_search.fit(Xtrain[lasso_cols], ytrain)

grid_search.best_params_

{'max_depth': 3, 'max_features': 11}

Best param trouvés : {'max_depth': 3, 'max_features': 11}

forest_reg = RandomForestRegressor(max_depth=3, max_features=13)

#train Random Forest on all train data
forest_reg.fit(Xtrain[lasso_cols], ytrain)

#print(forest_reg.feature_importances_)

#run the model on the test data to calcul prediction error 
print("Rrediction risk of Random Forest is : ",
      mean_squared_error(ytest, forest_reg.predict(Xtest[lasso_cols])))

print("R2 score of Random Forest is :", r2_score(
    ytest, forest_reg.predict(Xtest[lasso_cols])))

Rrediction risk of Random Forest is :  3998.430691111124
R2 score of Random Forest is : 0.39772634603694657


//anaconda3/lib/python3.7/site-packages/sklearn/ensemble/forest.py:245: FutureWarning: The default value of n_estimators will change from 10 in version 0.20 to 100 in 0.22.
  "10 in version 0.20 to 100 in 0.22.", FutureWarning)

Avec les hyperparamètres choisis par la validation croisée, on apprend le modèle avec tout les donées de training data, et ensuite on test le modèle sur les données test:

MSE for OLS 4574.783378254781 , MSE for RandomForest 3998.
R2 for OLS 0.31091177660371383 ,R2 score of Random Forest is : 0.39772634603694657
On voit que OLS est un modèle très simple mais efficace. Il évite bien le overfitting, donc le résultat de OLS sur les nouvelles données est assez correct - pas très loins du résultat de Random Forest.
OLS linéair est aussi beacoup plus perfermant que le modèle polynomial sur les données de test, car le modèle polynomial est souvent overfitted.