** Markov Chains and Hidden Markov Models **
Yang WANG
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
Partie I
On veut générer des mots dans une langue donnée en modélisant la formation de ces mots par une chaîne de Markov. Les 28 états du modèle correspondent aux 26 lettres de l’alphabet auxquelles et on ajoute un état ‘espace initial’ (état 1) et un état ‘espace final’ (état 28) qui sert à terminer les mots.
La correspondance entre la valeur numérique d’un état et un caractère est la suivante : l’état 1 correspond à un espace (avant le début d’un mot) et l’état 28 à celui d’un espace en fin de mot.
Les états 2 à 27 correspondent aux caractères de a à z. On pourra utiliser une structure de dictionnaire en python pour faire cette correspondance.
On utilisera une chaîne de Markov ergodique entre les 26 états correspondants aux lettres de l’alphabet.
1.2a Matrice de transitions
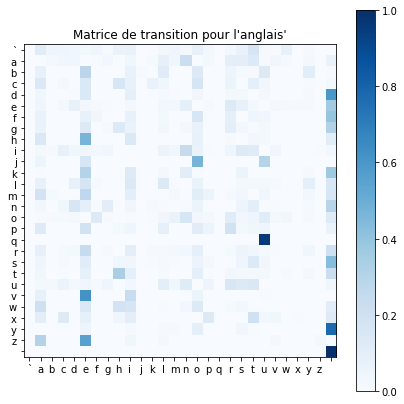
Le fichier bigramenglish.txt contient la matrice des transitions pour l’anglais (bigrams) entre deux symboles (caractères ou espaces). Le terme générique (i,j) de la matrice de transition correspond à la probabilité de transiter vers l’état j à partir de l’état i.
A quelles probabilités correspond la première ligne de la matrice de transition ? et celles de la dernière colonne ? Pour chaque lettre de l’alphabet, indiquer la transition la plus fréquente depuis cette lettre.
filename_A = 'Part1/bigramenglish.txt'
bi_eng = np.loadtxt(filename_A)
filename_B = 'Part1/bigramfrancais.txt'
bi_fr = np.loadtxt(filename_B)
bi_eng.shape
(28, 28)
#"Matrice de transition pour l'anglais'"
import matplotlib.cm as cm
plt.figure(figsize=(7, 7))
plt.xticks(range(28), [chr(97 + x-1) for x in range(27)])
plt.yticks(range(28), [chr(97 + x-1) for x in range(27)])
plt.imshow(bi_eng, cmap='Blues')
plt.colorbar()
plt.title("Matrice de transition pour l'anglais'")
Text(0.5, 1.0, "Matrice de transition pour l'anglais'")
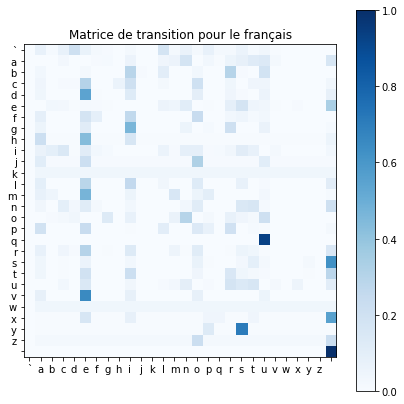
#"Matrice de transition pour le français"
plt.figure(figsize=(7, 7))
plt.xticks(range(28), [chr(97 + x-1) for x in range(27)])
plt.yticks(range(28), [chr(97 + x-1) for x in range(27)])
plt.imshow(bi_fr, cmap='Blues')
plt.colorbar()
plt.title("Matrice de transition pour le français")
Text(0.5, 1.0, 'Matrice de transition pour le français')
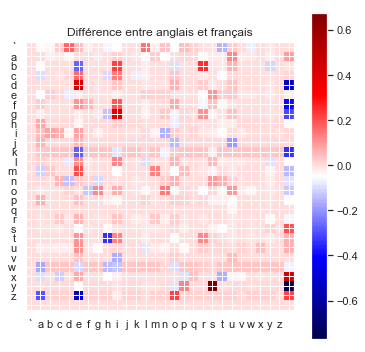
#"Différence entre anglais et français"
plt.figure(figsize=(6, 6))
plt.title("Différence entre anglais et français")
plt.xticks(range(28), [chr(97 + x-1) for x in range(27)])
plt.yticks(range(28), [chr(97 + x-1) for x in range(27)])
plt.imshow(bi_fr-bi_eng, cmap='seismic')
plt.colorbar()
<matplotlib.colorbar.Colorbar at 0x124a7ee10>
sns.set()
plt.figure(figsize=(14,4))
plt.bar([chr(97 + x-1) for x in range(28)], bi_eng[0],alpha=0.9,label='English')
plt.bar([chr(97 + x-1) for x in range(28)], bi_fr[0],alpha=0.3,label='Français')
plt.title('Les probabilités du début de mot')
plt.legend()
bi_eng[0, :]
array([0.0000000e+00, 1.1268720e-01, 4.3608943e-02, 4.5454545e-02,
3.2904451e-02, 2.2094495e-02, 4.1763341e-02, 1.5555790e-02,
6.4437882e-02, 6.8920059e-02, 3.6384729e-03, 4.2185193e-03,
2.3465514e-02, 3.9759544e-02, 2.2832736e-02, 7.0343809e-02,
3.1058848e-02, 1.4237503e-03, 2.5680236e-02, 6.6916262e-02,
1.6452225e-01, 1.0388104e-02, 7.0660198e-03, 7.0502004e-02,
1.0546298e-04, 1.0599030e-02, 5.2731491e-05, 0.0000000e+00])
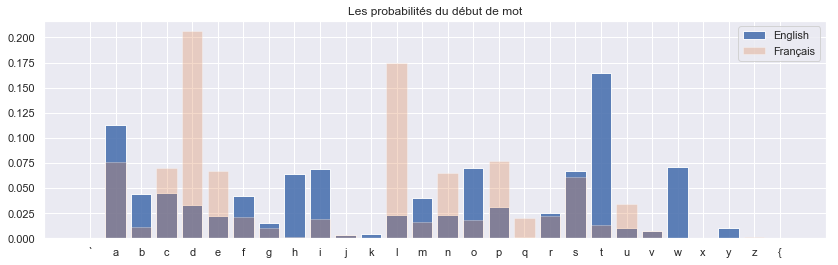
Les probabilités de la première ligne correspondent aux probabilitées de transitions en partant de l’état initial. La première valeur et la dernière valeur valent 0 qui signifie que l’état initial va forcement à un autre état sauf à l’état final. En anglais, on voit qu’il est très probable que les mots commencent par ‘t’,’a’,’w’. Alors qu’en français, il est plus probable que les mots commencent par ‘d’,’i’,’p’.
sns.set()
plt.figure(figsize=(14,4))
plt.bar([chr(97 + x-1) for x in range(28)], bi_eng[:, -1],label='English')
plt.bar([chr(97 + x-1) for x in range(28)], bi_fr[:, -1],alpha=0.3,label='Français')
plt.title('Les probabilités de la fin du mot')
plt.legend()
bi_eng[:, -1]
array([0.0000000e+00, 6.7478169e-02, 7.1084433e-03, 1.9535224e-02,
5.9884373e-01, 3.6047379e-01, 3.9653963e-01, 3.1566736e-01,
1.0300926e-01, 2.4606608e-02, 9.5877277e-04, 3.7225637e-01,
1.5338255e-01, 1.5795761e-01, 2.9421872e-01, 1.2308174e-01,
6.4222084e-02, 1.3966480e-03, 2.1088912e-01, 4.3030156e-01,
2.2273059e-01, 3.8466582e-02, 9.9108028e-05, 1.0216281e-01,
1.2345679e-01, 7.7582944e-01, 1.9193858e-03, 1.0000000e+00])
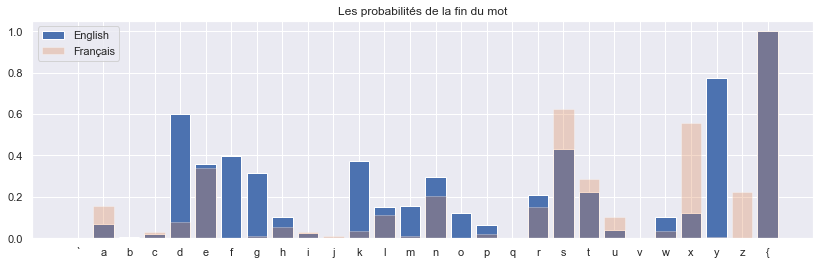
La dernière colonne correspondent aux probabilitées de transitions en partant de chaque état vers état final qui est un état absorbant, c’est ici les probabilitées de chaque lettre avec laquelle le mot se termine . En anglais, on voit que quand on a les lettres ‘d’,’s’,’y’, il est très probable que ce soit la fin du mot.
I2a Pour chaque lettre de l’alphabet, indiquer la transition la plus fréquente depuis cette lettre.
dic = {1: ' ',
2: 'a',
3: 'b',
4: 'c',
5: 'd',
6: 'e',
7: 'f',
8: 'g',
9: 'h',
10: 'i',
11: 'j',
12: 'k',
13: 'l',
14: 'm',
15: 'n',
16: 'o',
17: 'p',
18: 'q',
19: 'r',
20: 's',
21: 't',
22: 'u',
23: 'v',
24: 'w',
25: 'x',
26: 'y',
27: 'z',
28: ' '}
print('la transition la plus fréquente depuis chaque lettre(English):')
for i in range(len(bi_eng)):
print(i, dic[i+1], dic[np.argmax(bi_eng[i, :])+1])
la transition la plus fréquente depuis chaque lettre(English):
0 t
1 a n
2 b e
3 c o
4 d
5 e
6 f
7 g
8 h e
9 i n
10 j o
11 k
12 l e
13 m e
14 n
15 o n
16 p e
17 q u
18 r e
19 s
20 t h
21 u r
22 v e
23 w a
24 x t
25 y
26 z e
27
On voit beaucoup de pattern dans l’anglais ici tels que : th , an , co , in, etc.
Le début de mot le plus fréquent est ‘t’, comme ‘tea’.
print('la transition la plus fréquente depuis chaque lettre(Français):')
for i in range(len(bi_fr)):
print(i, dic[i+1], dic[np.argmax(bi_fr[i, :])+1])
la transition la plus fréquente depuis chaque lettre(Français):
0 d
1 a n
2 b r
3 c e
4 d e
5 e
6 f i
7 g i
8 h e
9 i c
10 j o
11 k a
12 l e
13 m e
14 n
15 o n
16 p e
17 q u
18 r e
19 s
20 t
21 u r
22 v e
23 w a
24 x
25 y s
26 z o
27
On voit beaucoup de pattern dans le français ici tels que : br, fi, me, de, etc.
1.2b Générer un mot
On veut générer un mot à partir de l’état initial 1 (espace de début de mot).
Ecrire une fonction etat_suivant qui génère un état (à t+1) à partir de l’état courant (à t) et à l’aide de la matrice de transitions et de la fonction de répartition.
def etat_suivant(dic, bi_gram, state):
unif = np.random.random()
line = bi_gram[state-1]
thr = np.where(np.cumsum(line) > unif)[0][0]+1
return thr
Afficher sur un graphique la fonction de répartition pour une ligne de la matrice de transition et expliquer son rôle pour la génération de l’état à t+1.
sns.set()
plt.figure(figsize=(12, 6))
for i in range(3):
plt.plot(np.cumsum(bi_eng[i]))
plt.title("Cumulative Distribution function")
unif = np.random.random()
print(unif)
plt.plot([0, 28], [unif, unif], c='red')
plt.show()
0.4110689239561004
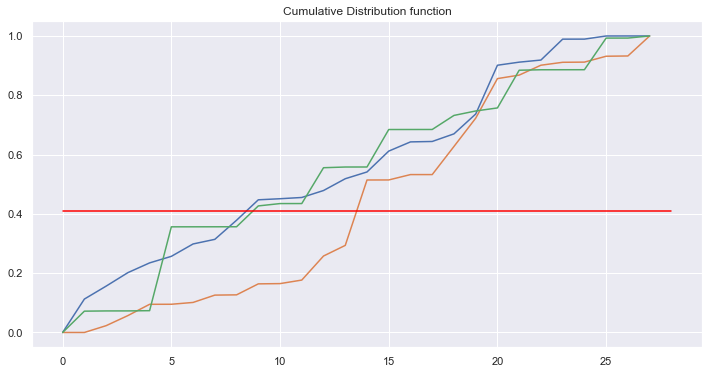
La fonction cumulative de distribution permet de savoir quel chiffre tirer par la suite. D’abord on tire de manière aléatoire uniforme, puis on compare avec la distribution cumulative.
Utiliser cette fonction pour écrire la fonction genere_state_seq qui génère une séquence d’états jusqu’à aboutir à l’état final (28).
def genere_state_seq(dic, bi_gram):
state = 1
seq = []
states = []
while state != 28:
state = etat_suivant(dic, bi_gram, state)
states.append(state)
return states
def display_seq(letter, bi_eng):
word = []
seq = []
while len(word) < 2:
word = genere_state_seq(letter, bi_eng)
# print(word)
seq = [dic[s] for s in word]
# print(seq)
return ''.join(seq)
Utiliser ces fonctions pour générer des mots et donner des exemples de mots générés.
for i in range(25):
print(display_seq(i, bi_eng))
ofickn
m
anliethagedide
to
ry
t
amondizat
ivanangangheenyorcken
iviman
ngutonghir
wad
athotanon
p
angheded
e
d
f
fronge
pes
prtched
an
ad
trtalls
hedemiegik
tentremen
Remarque sur les lettres seules:
Les mots anglais termininent souvent avec ‘s’,’y’,’d’,’f’, si depuis l’état initial on tombe sur un ‘s’, il y a grande chance que cela termine tout de suite avec l’état final.
1.2.c Générer une phrase
On veut générer une suite de mots (phrase). Créer un état final de phrase (état 29, correspondant au caractère . ) dont la probabilité de transition vers cet état depuis un état final de mot est 0.1. Ecrire une fonction modifie_mat_dic qui modifie la matrice de transition et le dictionnaire en conséquence. Donner des exemples de phrases générées.
def modify_mat_dic(bi_eng):
# Append new column
new_col = (np.zeros(28)).T
bi_eng = np.vstack((bi_eng, new_col))
# Append new line
new_line = np.zeros(29).reshape(-1, 1)
bi_eng = np.hstack((bi_eng, new_line))
bi_eng[-1, -1] = 1
# Modify before last line
bi_eng[-2] = np.zeros(29)
bi_eng[-2, 0] = 0.9
bi_eng[-2, -1] = 0.1
return bi_eng
On crée la probabilié que un état final de mot transit vers l’état initial du mot (générer le mot suivant), ainsi la probabilié que un état final de mot transit vers la fin de phrase, cette probabilité contrôle la longeur moyenne des phrases.
bi_eng_mod = modify_mat_dic(bi_eng)
dic_2 = {1: ' ',
2: 'a',
3: 'b',
4: 'c',
5: 'd',
6: 'e',
7: 'f',
8: 'g',
9: 'h',
10: 'i',
11: 'j',
12: 'k',
13: 'l',
14: 'm',
15: 'n',
16: 'o',
17: 'p',
18: 'q',
19: 'r',
20: 's',
21: 't',
22: 'u',
23: 'v',
24: 'w',
25: 'x',
26: 'y',
27: 'z',
28: '',
29: '.'}
def genere_state_seq_2(dic, bi_gram):
state = 1
seq = []
while state != 29:
state = etat_suivant(dic, bi_gram, state)
seq.append(dic[state])
return ''.join(seq)
print("English:")
for i in range(20):
print(genere_state_seq_2(dic_2, bi_eng_mod))
English:
t owar y trempious upon whasthe gh stu t d led te indaiche hey wanthoofind omulingoure m councavepan anlie m y gemenedis woritherupld.
o cthiareriothentho eliseles d aigas pandint om.
tisurare jetheds ferms halere ay thas s ler haterkedequlvea but d ole coveanemetrng and momatiaperct thld celal aclomungrabadinlixtrarot s imiocouconglitifanthe arthe fishin ca tondg tis.
sfins d than ther ictechindethre.
ilylf he manan ric fousis wricond al aitogenstof.
s aly at f dofan licailed pesathin ist be f satemeifone aje w tope t ous huthatefoulind gld.
thaver iof.
oo was wale ste te in.
meroverathed s y stouraliere an thed.
ca ar.
n rar the s ioraret d dsaigubr athino usw tebet tandedd plysans seres hinghenchesere migiga.
cond on ear.
ivan t ande folldure re sliss e t anan int thee allas sthed are t thibusldind fave wh dothem crrd ofurmio pllitsed ptthalde athrivil ouey ceren.
s ameastin rizawemis pr tor d tir thear was ases jofeseed che ngitherie tin we.
tol icacosofothe tinth bond asucewaun.
g fon heye tiseounas llise l hosmuth.
meng o s co ited t rist s iof int h dshlillerepld mpree l ted ay t kede t.
washtru waswetal pt r add o aup t otipreent danged ovead orcy skexvinthadrn s.
a tharthioy sty histere.
terory e f me d.
bi_fr_mod = modify_mat_dic(bi_fr)
print("Français:")
for i in range(20):
print(genere_state_seq_2(dic_2, bi_fr_mod))
Français:
s pograutreucenutis libansotprire nen debrencieupe le lit stilanonnlons duet qu estit.
atiompas delicice des libicen cialeointsasunsten recicions stures roic es ls dele.
prnouichestron vellicequtuxppuerticices poui te lis.
ane nteresurt de.
libivirarrnsens ecoutrcens brs entioue cutononos e elauve de.
ls peus demblas es te ou e ansouequnse le con l grmmelie cauesianouc difibux donche mempprodintogn acocourencexestialau oriblicis s plonsodes lioncoulanttex a.
lirencencoues ns oiobrest pa qur lebrt n cinepalene ait ce anojatil d drceterie leprorance n deret ie des debux ens te.
zopancope anebqurapes lin pamos rte des n bicts des ns pes par.
l denache dovifoniars eut outige gieremys n s ess.
licemmmogeston los.
logrutroue ceces ont ceneus tas lans durastintrenonemeunex plintitepppou n.
lavens me cons daleciogi.
llec d dot pavauvenstoun liomins gelive fictefit cod da a de denes s sux s domute ftexe.
demanciastes peve ls l de.
ilicormpars ppappe dendans.
de.
dibux ansite n.
daniammppogre les codestil cos pe sacibis e utess prele ns jomeste pr paire a ie litiaue le autce.
ver aun e nfap dontiticus perouteebure iedapl nuerountre detistedevr les dibus cerine lodebramue nt s liemerls d t e durt.
ve.
1.3 Reconnaissance de la langue
Charger la matrice des transitions entre caractères pour le français. Ecrire une fonction calc_vraisemblance qui calcule la vraisemblance du modèle français pour une phrase donnée en multipliant les probabilités de transition. Pour tenir compte de toutes les transitions (notamment celles entre espaces de fin et de début de mots et vers la fin de phrase) on pourra transformer (manuellement) une séquence « mot1 mot2.» par la séquence « -mot1+-mot2+.», les signes - , + et . représentant l’état initial de mot, l’état final de mot et l’état final de phrase, respectivement.
dic_3 = {1: '-',
2: 'a',
3: 'b',
4: 'c',
5: 'd',
6: 'e',
7: 'f',
8: 'g',
9: 'h',
10: 'i',
11: 'j',
12: 'k',
13: 'l',
14: 'm',
15: 'n',
16: 'o',
17: 'p',
18: 'q',
19: 'r',
20: 's',
21: 't',
22: 'u',
23: 'v',
24: 'w',
25: 'x',
26: 'y',
27: 'z',
28: '+',
29: '.'}
# use reversed dictionary
dic_3_inv = {v: k for k, v in dic_3.items()}
def calc_vraisemblance(dic, bi_eng, bi_fr, seq):
key0 = 0
trans_eng = 1
trans_fra = 1
for letter in seq:
key1 = dic_3_inv[letter]-1
if (key0 == 0) & (key1 == 0):
pass
else:
trans_eng = trans_eng * bi_eng[key0, key1]
trans_fra = trans_fra * bi_fr[key0, key1]
key0 = dic_3_inv[letter]-1
if trans_eng > trans_fra:
print("It's English !")
else:
print("C'est Français!")
return trans_eng, trans_fra
Calculer la vraisemblance des modèles français et anglais pour la phrase « to be or not to be ». De même calculer la vraisemblance des modèles français et anglais pour la phrase « etre ou ne pas etre ».
calc_vraisemblance(dic_3, bi_eng_mod, bi_fr_mod, '-to+-be+-or+-not+-to+-be+.')
It's English !
(8.112892227809415e-20, 5.9602081018686406e-30)
calc_vraisemblance(dic_3, bi_eng_mod, bi_fr_mod, '-to+-be+-or+-not+-to+-be+.')
It's English !
(8.112892227809415e-20, 5.9602081018686406e-30)
calc_vraisemblance(dic_3, bi_eng_mod, bi_fr_mod, '-etre+-ou+-ne+-pas+-etre+.')
C'est Français!
(4.462288711775253e-24, 1.145706887234789e-19)
calc_vraisemblance(dic_3, bi_eng_mod, bi_fr_mod, '-etre+-ou+-ne+-pas+-etre+.')
C'est Français!
(4.462288711775253e-24, 1.145706887234789e-19)
Part II
L’objectif de cette partie est de générer des séquences d’observations suivant un modèle de Markov Caché donné, puis de calculer la vraisemblance d’une séquence d’observations suivant un modèle de Markov Caché donné.
Le modèle de Markov est de type discret.
Les classes de caractères (classes 0, 1,…, 7 dans la base MNIST) sont modélisées chacune par un modèle à Q=5 états de type gauche-droite.
- Les états 1 et 5 correspondent à des colonnes de pixels de type fond de l’image (niveau 0).
- Les états 2, 3 et 4 correspondent au début, milieu et fin du caractère respectivement.
- Les transitions entre états sont indiquées dans la matrice de transitions A de taille QxQ.
- Les vecteurs π sont tous égaux à π=(1 0 0 0 0). Les séquences d’états commencent donc toujours par l’état q1=1.
A0 = np.loadtxt('Part2/A0.txt')
B0 = np.loadtxt('Part2/B0.txt')
Pi0 = np.loadtxt('Part2/vect_pi0.txt')
print(A0.shape, B0.shape, Pi0.shape)
Pi0
(5, 5) (32, 5) (5,)
array([1., 0., 0., 0., 0.])
Les séquences d’observations sont discrètes et issues d’images de chiffres de la base MNIST. Les séquences d’observations consistent en séquences d’index (symboles) des éléments du dictionnaire.

Ce dictionnaire est stocké sous forme matricielle (matrice v).
filename='Part2/matrice_symboles.txt'
v = np.loadtxt(filename)
v.shape
(5, 32)
L’élément numéro i d’une séquence d’observations correspond au symbole i et donc à la colonne i de la matrice v. Un symbole correspond à une configuration de colonne de 5 pixels (binaires : noir/blanc). Il y a 2^5=32 configurations, et donc symboles possibles.
plt.figure(figsize=(12,8))
plt.imshow(v, 'gray')
plt.show()
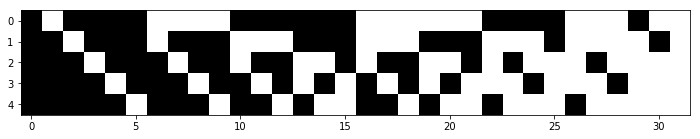
Une séquence d’observations correspondant à l’image simplifiée de la fig. 1 est : [1 1 1 1 1 1 14 23 23 27 18 18 18 12 12 12 12 12 12 12 23 23 23 14 4 1 1 1]
La concaténation des éléments du dictionnaire correspondant aux index de la séquence d’observations peut être visualisée sous forme d’image en remplaçant chaque index par le vecteur de pixels correspondant dans le dictionnaire
Les probabilités des observations dans chaque état sont indiquées dans la matrice B (32 lignes, 5 colonnes).
B0.shape
(32, 5)
np.round(B0,2)
array([[ 1. , -0. , -0. , -0. , 1. ],
[-0. , 0. , 0. , 0. , -0. ],
[-0. , 0. , 0. , 0.02, -0. ],
[-0. , 0.08, 0. , 0.13, -0. ],
[-0. , 0.01, 0.02, 0. , -0. ],
[-0. , 0. , 0. , 0. , -0. ],
[-0. , 0. , 0. , 0. , -0. ],
[-0. , 0. , 0. , 0. , -0. ],
[-0. , 0. , 0.02, 0. , -0. ],
[-0. , 0. , 0. , 0. , -0. ],
[-0. , 0.02, 0. , 0.16, -0. ],
[-0. , 0. , 0.32, 0. , -0. ],
[-0. , 0. , 0. , 0. , -0. ],
[-0. , 0.22, 0. , 0.05, -0. ],
[-0. , 0. , 0. , 0. , -0. ],
[-0. , 0. , 0. , 0. , -0. ],
[-0. , 0. , 0. , 0.02, -0. ],
[-0. , 0. , 0.45, 0. , -0. ],
[-0. , 0. , 0. , 0. , -0. ],
[-0. , 0. , 0. , 0. , -0. ],
[-0. , 0. , 0. , 0. , -0. ],
[-0. , 0. , 0. , 0. , -0. ],
[-0. , 0.57, 0. , 0.5 , -0. ],
[-0. , 0.02, 0.01, 0. , -0. ],
[-0. , 0. , 0. , 0. , -0. ],
[-0. , 0.01, 0. , 0. , -0. ],
[-0. , 0. , 0.07, 0.11, -0. ],
[-0. , 0. , 0.09, 0. , -0. ],
[-0. , 0. , 0. , 0. , -0. ],
[-0. , 0.07, 0. , 0. , -0. ],
[-0. , 0. , 0. , 0. , -0. ],
[-0. , 0. , 0.01, 0. , -0. ]])
plt.imshow(B0.T)
<matplotlib.image.AxesImage at 0x11686e320>

II.2 Génération de séquences d’observations
II 2.1 A quoi correspondent les zéros de la matrice B ? et ceux de la matrice A et du vecteur π?
-
Les 0 de la matrice B correspondent aux probabilités nulles d’observation dans un état donné.Par example, il n’y a pas de sympol 2 dans l’état 1 (fond de l’image).
-
Les 0 de la matrice A signifie qu’il n’y a pas de possibilité de transition d’un état à l’autre.
-
Les 0 du vecteur π correspondent au fait que l’on commence toujours à l’état 1.
II.2.2 Ecrire une fonction etat_suivant qui génère un état qt+1(à t+1) à partir de l’état courant qt (à t) à l’aide de la matrice de transitions et de la fonction de répartition cumsum.
A0
array([[ 0.84178118, 0.15821882, -0. , -0. , -0. ],
[-0. , 0.7886163 , 0.2113837 , -0. , -0. ],
[-0. , -0. , 0.86339743, 0.13660257, -0. ],
[-0. , -0. , -0. , 0.79150194, 0.20849806],
[-0. , -0. , -0. , -0. , 1. ]])
def etat_suivant(state, A):
unif = np.random.random()
repar = np.cumsum(A[state-1])
state_next = 0
while unif >= repar[state_next]:
state_next = state_next+1
return state_next+1
Afficher la fonction de répartition pour une ligne de la matrice de transition et expliquer son rôle pour la génération de l’état à t+1.
sns.set()
plt.figure(figsize=(5, 5))
plt.plot(np.cumsum(A0[0]))
plt.plot(np.cumsum(A0[1]))
plt.plot(np.cumsum(A0[2]))
unif = np.random.random()
print(unif)
plt.plot([0, 4], [unif, unif], c='red')
plt.title("Cumulative Distribution function")
plt.show()
0.18148519881892022
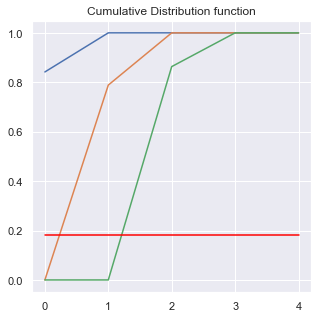
La fonction cumulative de distribution permet de savoir quel état tirer par la suite. D’abord on tire de manière aléatoire uniforme, puis on compare avec la distribution cumulative.
II.2.3 Générer une séquence d’observations suivant le modèle de Markov Caché du chiffre 0. On commencera par générer une séquence d’états suivant ce modèle à l’aide de la fonction etat_suivant. Puis on générera la séquence d’observations par le même procédé.
def symbole(state, B):
unif = np.random.random()
repar = np.cumsum(B[:, state-1])
symbole = 0
while unif >= repar[symbole]:
symbole = symbole+1
return symbole+1
sequence = [1]
q = 1
ob=[]
while q != 5:
q = etat_suivant(q, A0)
ob.append(symbole(q, B0))
sequence.append(q)
print('état',sequence)
print('observation',ob)
état [1, 1, 1, 1, 1, 1, 1, 2, 2, 3, 3, 3, 3, 3, 4, 5]
observation [1, 1, 1, 1, 1, 1, 14, 4, 12, 12, 18, 18, 5, 23, 1]
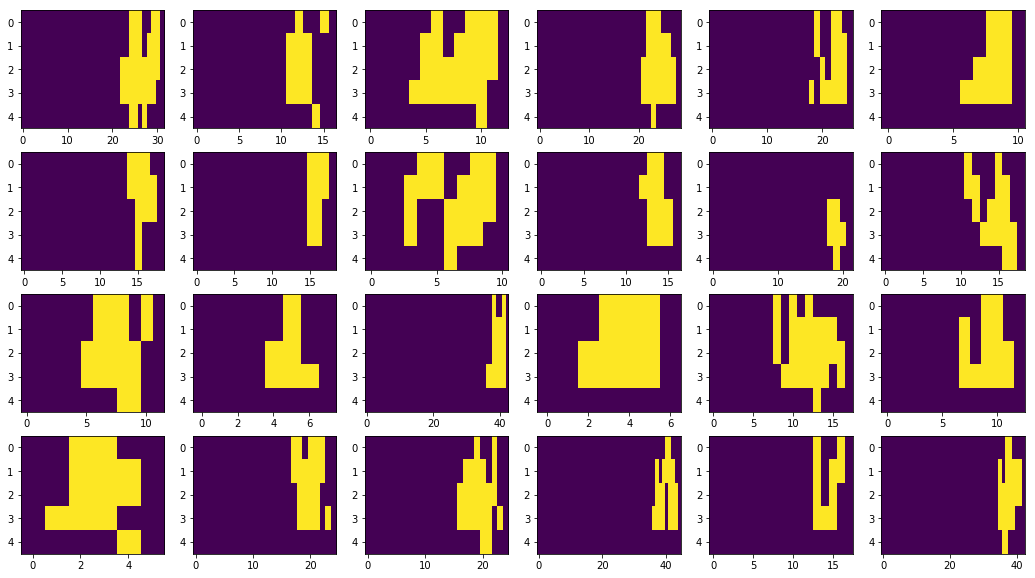
II.2.4 Visualiser le résultat sous forme d’image. Générer des séquences pour le chiffre 7 et le chiffre 1 (matrices B1.txt, B7.txt, etc…)
im = np.array([v[:, symbole(x, B0)-1] for x in sequence]).T
plt.imshow(im, interpolation='none', aspect='auto')
<matplotlib.image.AxesImage at 0x1a29c5aef0>
fig, axes = plt.subplots(4, 6, figsize=(18, 10))
for i, ax in enumerate(axes.flat):
sequence = [1]
q = 1
while q != 5:
q = etat_suivant(q, A0)
sequence.append(q)
# print(sequence)
im = np.array([v[:, symbole(x, B0)-1] for x in sequence]).T
ax.imshow(im, interpolation='none', aspect='auto')

# 1111111
A1 = np.loadtxt('Part2/A1.txt')
B1 = np.loadtxt('Part2/B1.txt')
Pi1 = np.loadtxt('Part2/vect_pi1.txt')
fig, axes = plt.subplots(4, 6, figsize=(18, 10))
for i, ax in enumerate(axes.flat):
sequence = [1]
q = 1
while q != 5:
q = etat_suivant(q, A1)
sequence.append(q)
# print(sequence)
im = np.array([v[:, symbole(x, B1)-1] for x in sequence]).T
ax.imshow(im, interpolation='none', aspect='auto')
# 7777777
A7 = np.loadtxt('Part2/A7.txt')
B7 = np.loadtxt('Part2/B7.txt')
Pi7 = np.loadtxt('Part2/vect_pi7.txt')
fig, axes = plt.subplots(4, 6, figsize=(18, 10))
for i, ax in enumerate(axes.flat):
sequence = [1]
q = 1
while q != 5:
q = etat_suivant(q, A7)
sequence.append(q)
# print(sequence)
im = np.array([v[:, symbole(x, B7)-1] for x in sequence]).T
ax.imshow(im, interpolation='none', aspect='auto')

II.3 Calcul de la vraisemblance de séquences d’observations
Les fichiers SeqTest0.txt, SeqTest1.txt, SeqTest7.txt contiennent chacun 10 séquences d’observations de chiffres des 3 classes 0, 1 et 7, disposés en ligne. Le script suivant extrait la 5ème observation de la 3ème séquence des chiffres 0.
filename = 'Part2/SeqTest0.txt'
TestChiffres = np.loadtxt(filename)
TestChiffres1 = np.loadtxt('Part2/SeqTest1.txt')
TestChiffres7 = np.loadtxt('Part2/SeqTest7.txt')
nex = 2
seq = TestChiffres[nex, :]
seq
array([ 1., 1., 1., 1., 1., 4., 14., 14., 23., 23., 23., 23., 23.,
23., 23., 23., 23., 23., 23., 23., 23., 11., 11., 4., 4., 1.,
1., 1.])
i=4
im = np.array([v[:,int(x)-1] for x in TestChiffres[2]]).T
plt.imshow(im, interpolation='none', aspect='auto')
<matplotlib.image.AxesImage at 0x1250465f8>

II3.1 Calculer la vraisemblance de ces séquences suivant chacun des modèles (0, 1 et 7) par l’algorithme de Viterbi (on pourra implémenter la version logarithmique de cet algorithme). Pour cela les matrices A, B et π seront converties en logarithmes (utiliser np.log).
def viterbi_log(A, B, C, Obs_seq):
I = A.shape[0] # number of states
N = Obs_seq.shape[1] # length of observation sequence
# compute log probabilities
tiny = np.finfo(0.).tiny
A_log = np.log(A + tiny)
C_log = np.log(C + tiny)
B_log = np.log(B + tiny)
# initialize D and E matrices
D_log = np.zeros([I, N])
E = np.zeros([I, N-1])
D_log[:, 0] = C_log + B[:, 0]
# compute D and E in a nested loop
for n in range(1, N):
for i in range(I):
temp_sum = A_log[:, i] + D_log[:, n-1]
D_log[i, n] = np.amax(temp_sum) + B_log[i, int(Obs_seq[0, n])-1]
E[i, n-1] = np.argmax(temp_sum)
max_ind = np.zeros([1, N])
max_ind[0, -1] = np.argmax(D_log[:, -1])
vraisemblance = np.max(D_log[:, -1])
#print("The log likelihood with Viterbi is", vraisemblance)
# Backtracking
for n in range(N-2, 0, -1):
max_ind[0, n] = E[int(max_ind[0, n+1]), n]
# Convert zero-based indices to state indices
S_opt = max_ind.astype(int)+1
return vraisemblance, S_opt
# Apply Viterbi algorithm
Obs_seq = np.array([TestChiffres[0]])
vraisemblance, S_opt = viterbi_log(
A0.T, B0.T, Pi0, np.array([TestChiffres[1]]))
print("The log likelihood with Viterbi is", vraisemblance)
# print('Observation sequence: '+str([int(x) for x in TestChiffres[3]]))
print('Observation sequence: '+str(TestChiffres[0].astype(int)))
print('Optimal state sequence: '+str(S_opt))
The log likelihood with Viterbi is -746.8849317113572
Observation sequence: [ 1 1 1 1 1 1 14 14 14 23 12 12 12 12 18 18 18 18 18 18 23 23 14 1
1 1 1 1]
Optimal state sequence: [[1 1 1 1 1 4 4 4 4 4 4 3 3 3 3 3 3 3 3 2 2 2 2 1 1 1 1 1]]
II.3.2 Donner le résultat de la classification des images de test en considérant un problème à trois classes : 0, 1 et 7.
def classifier(seq):
# calculate the likelihood
score_0, _ = viterbi_log(A0.T, B0.T, Pi0, np.array([seq]))
score_1, _ = viterbi_log(A1.T, B1.T, Pi1, np.array([seq]))
score_7, _ = viterbi_log(A7.T, B7.T, Pi7, np.array([seq]))
score = [score_0, score_1, score_7]
# print(score_0,score_1,score_7)
if np.argmax([score_0, score_1, score_7]) == 0:
print("Classified as 0")
if np.argmax([score_0, score_1, score_7]) == 1:
print("Classified as 1")
if np.argmax([score_0, score_1, score_7]) == 2:
print("Classified as 7")
print("TestChiffres 0:")
for seq in TestChiffres:
classifier(seq)
TestChiffres 0:
Classified as 0
Classified as 0
Classified as 0
Classified as 0
Classified as 0
Classified as 0
Classified as 0
Classified as 0
Classified as 0
Classified as 0
print("TestChiffres 1:")
for seq in TestChiffres1:
classifier(seq)
TestChiffres 1:
Classified as 1
Classified as 1
Classified as 1
Classified as 1
Classified as 1
Classified as 1
Classified as 1
Classified as 0
Classified as 1
Classified as 1
# We visualize the misclassified number
im = np.array([v[:, int(x)-1] for x in TestChiffres1[7]]).T
plt.imshow(im, interpolation='none', aspect='auto')
<matplotlib.image.AxesImage at 0x1202f2ac8>

print("TestChiffres 1:")
for seq in TestChiffres7:
classifier(seq)
TestChiffres 1:
Classified as 7
Classified as 7
Classified as 1
Classified as 7
Classified as 7
Classified as 7
Classified as 7
Classified as 7
Classified as 7
Classified as 7
# We visualize the misclassified number
im = np.array([v[:,int(x)-1] for x in TestChiffres7[2]]).T
plt.imshow(im, interpolation='none', aspect='auto')
<matplotlib.image.AxesImage at 0x122c33a20>

Dans les fichiers test, les séquences sont généralement bien classés dans chaque classe, sauf 2 cas que j’affiche ici. Il est vrai que ces 2 chiffres sont un peu déformés.