KNN
11/27/2019
- Yang WANG
Imports
import numpy as np
import matplotlib.pyplot as plt
from tpknnsource import (rand_gauss, rand_bi_gauss, rand_checkers, rand_tri_gauss,
rand_clown, plot_2d, ErrorCurve,
frontiere_new, LOOCurve)
import numpy as np
from scipy import stats
from sklearn.neighbors import KNeighborsClassifier
from sklearn.base import BaseEstimator, ClassifierMixin
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib import rc
from sklearn import linear_model
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import accuracy_score
from sklearn import linear_model
Settings
# Plot
plt.close('all')
rc('font', **{'family': 'sans-serif', 'sans-serif': ['Computer Modern Roman']})
params = {'axes.labelsize': 12,
'font.size': 16,
'legend.fontsize': 16,
'text.usetex': False,
'figure.figsize': (8, 6)}
plt.rcParams.update(params)
# Seaborn
sns.set_context("poster")
sns.set_palette("colorblind")
sns.set_style("white")
sns.axes_style()
# Seed initialization
np.random.seed(seed=44)
# For saving files
saving_activated = True # False
Data Generation: Examples
1) Étudiez les fonctions rand_bi_gauss, rand_tri_gauss, rand_clown et rand_checkers. Que ren- voient ces fonctions ? À quoi correspond la dernière colonne ? Générez les données en utilisant chaque de ces 4 fonctions avec les paramètres du corrigé du TP1 (pour rand_checkers prenez 150 pour les deux premiers arguments; pour rand_tri_gauss générez 50 observations dans chaque classe, centrées en (1,1)⊤, (−1,−1)⊤ et (1,−1)⊤, tous les écart-types égaux à 0.9). On va nommer ces jeux de données #1, #2, #3 et #4, respectivement.
From rand_gauss
n = 10
mu = [1., 1.]
sigmas = [1., 1.]
rand_gauss(n, mu, sigmas)
array([[ 0.24938528, 2.31635732],
[ 2.24614003, -0.60491574],
[-0.46814368, -0.71507046],
[ 2.85878369, 1.08758798],
[ 0.9476778 , 1.55547164],
[ 0.03659631, 0.81967853],
[-0.18340916, 1.60544592],
[ 0.04834945, 1.36085606],
[ 2.06061026, 0.88284782],
[ 1.82566485, -0.20981355]])
From rand_bi_gauss
n1 = 20
n2 = 20
mu1 = [1., 1.]
mu2 = [-1., -1.]
sigmas1 = [0.9, 0.9]
sigmas2 = [0.9, 0.9]
X1, y1 = rand_bi_gauss(n1, n2, mu1, mu2, sigmas1, sigmas2)
rand_bi_gauss()
(array([[-0.93729995, -0.98958643],
[-0.84079037, -0.94502372],
[-0.93002651, -0.87087196],
[ 1.10600871, 1.11185812],
[-1.1402696 , -1.11923282],
[ 0.97938742, 0.92108496],
[ 1.0881702 , 0.80499798],
[ 1.12934226, 1.03908531],
[-0.84946165, -1.06300955],
[-1.07257053, -1.068453 ],
[-0.88813333, -1.10788531],
[-1.02965731, -0.94179026],
[-1.11511573, -1.05798733],
[-0.9982237 , -0.95044763],
[ 0.98989909, 0.96593905],
[-0.99479668, -1.05316003],
[-0.95420525, -0.96171559],
[-1.01603736, -1.07386721],
[ 1.02797223, 0.89002528],
[-0.89261177, -1.08092745],
[ 1.03364971, 0.93108528],
[ 1.06062442, 1.00033252],
[ 0.88208555, 1.04649081],
[-1.00865527, -1.09237986],
[-0.97977824, -1.06778816],
[-0.94345402, -0.95862746],
[ 0.96921092, 1.09343756],
[ 0.83146381, 0.99990225],
[ 1.05709328, 1.00877429],
[ 1.0162278 , 0.93410279],
[ 1.02138437, 0.90770031],
[-0.90768374, -1.0657499 ],
[-1.07104762, -1.2566515 ],
[ 0.9891463 , 0.96893515],
[-0.91736764, -0.85735093],
[-0.97456546, -0.78164844],
[-0.91064841, -1.01614351],
[-1.11865101, -0.85104347],
[-1.15763993, -0.98068986],
[ 1.11003777, 0.84740834],
[-1.02994347, -0.94942251],
[-0.92742866, -0.8251879 ],
[ 0.91373329, 0.97131911],
[-0.84520085, -0.98167382],
[-1.01765952, -1.06321876],
[ 0.90778967, 0.90518677],
[-1.04874739, -0.98609836],
[ 1.06307516, 1.10763895],
[-1.0718102 , -0.92382146],
[ 0.91905085, 1.04247809],
[-0.94153805, -1.10461062],
[ 1.10884268, 1.00568889],
[-0.99953073, -0.89183825],
[-0.99143183, -1.04804549],
[-1.22509465, -0.92402476],
[-1.0371156 , -1.03279957],
[ 1.09614281, 1.13800087],
[ 0.5789476 , 1.02709336],
[-0.97924355, -1.10377328],
[-0.95169427, -0.9720244 ],
[-0.93506166, -0.93949647],
[ 1.12118528, 1.1081193 ],
[-1.08410253, -1.02493904],
[ 1.1220941 , 1.01582537],
[ 0.75119708, 0.98250633],
[ 0.99659163, 0.9307617 ],
[ 1.11435842, 1.2613585 ],
[-1.02408111, -1.04802157],
[ 1.09768465, 0.9496141 ],
[ 1.04348687, 1.14833479],
[ 1.09197223, 0.99842747],
[ 1.07800123, 1.01756101],
[-1.01415065, -1.01298084],
[-1.042427 , -1.11986441],
[ 0.95673757, 0.98885503],
[-1.10820086, -1.12540414],
[ 0.9969666 , 1.25074334],
[-1.03928802, -1.04486162],
[-1.06224578, -1.16559716],
[-1.09956852, -0.97723823],
[ 1.07550487, 0.88025085],
[ 0.84949096, 0.96271458],
[-0.96808142, -0.99605295],
[ 0.90274616, 0.96942116],
[ 1.10922553, 0.82673391],
[ 0.86215488, 1.05563072],
[-1.03008592, -0.90180927],
[ 0.95117784, 1.17827044],
[-0.96581651, -0.93127589],
[ 1.01694168, 1.09723819],
[-0.98313487, -0.91477311],
[ 1.00981653, 0.85744275],
[-1.2074855 , -0.88412327],
[ 0.93433642, 1.09073431],
[-0.93662274, -0.90518498],
[-1.12208458, -0.98473526],
[ 0.94713783, 1.2206299 ],
[-1.06509512, -0.88392916],
[ 1.04478724, 1.12054422],
[-0.88111967, -0.93574179],
[ 1.09969137, 1.12638372],
[ 1.08997586, 0.94751659],
[ 1.02703341, 0.92884327],
[-0.9412884 , -1.11359069],
[-1.05486029, -0.88836903],
[ 0.7625061 , 0.91673208],
[-1.19989883, -1.11123129],
[ 1.20860598, 1.07289775],
[-0.98880002, -1.01828606],
[ 0.99226524, 0.88795382],
[ 0.98124604, 1.04161743],
[-1.06304993, -1.17721605],
[ 0.93604453, 0.90651505],
[-0.96740043, -0.97715034],
[ 0.98142459, 1.03904963],
[-1.04809499, -0.89420405],
[-0.90799834, -0.91407141],
[ 0.86305393, 0.98941079],
[ 0.98590835, 1.0210285 ],
[-0.93550204, -0.95733688],
[ 0.99463582, 1.0831982 ],
[-0.94922726, -0.97252495],
[ 0.93624516, 1.05004031],
[-0.88412119, -0.90519384],
[ 0.95213079, 0.95318276],
[ 0.92283183, 0.97458241],
[ 1.04333701, 1.1030371 ],
[ 0.91658017, 0.92134859],
[-1.31349829, -1.1689285 ],
[ 0.88646263, 0.82972065],
[-1.09154204, -1.00170118],
[-1.01812351, -0.90597731],
[-1.10835766, -0.89751765],
[ 1.05906539, 0.89448739],
[-1.04327878, -1.0420256 ],
[ 1.14522977, 0.91667236],
[ 1.17457413, 1.01101871],
[ 1.21801219, 1.045439 ],
[ 1.11303286, 1.02023919],
[-0.93487673, -0.95162923],
[-1.00539836, -1.06707031],
[ 0.97356211, 0.99342037],
[-0.9600897 , -0.92590829],
[-0.89054224, -0.94482934],
[-0.98332383, -1.10301142],
[-1.11762226, -0.93680577],
[-1.00863541, -1.01405372],
[ 1.03659198, 0.93296026],
[ 1.03021249, 0.90026432],
[ 0.9555221 , 1.25174649],
[-0.9826237 , -0.97791 ],
[-1.07492794, -0.88871846],
[-0.93378501, -0.96772311],
[ 0.98594997, 1.03403191],
[-0.84626859, -0.96532757],
[ 0.86864087, 1.11341978],
[ 1.13086162, 1.25196152],
[ 0.89531423, 1.02011059],
[ 0.94414011, 1.15710327],
[ 1.11330393, 1.05201976],
[-1.02075592, -1.05537305],
[-1.10964184, -0.94824553],
[ 0.96498364, 1.05610259],
[ 0.96258998, 1.10614331],
[ 0.90339606, 1.08090137],
[ 0.87888334, 0.85732611],
[ 0.86668443, 0.93918194],
[ 1.15721027, 0.99944159],
[ 0.97869915, 0.922265 ],
[-0.90663462, -1.09858231],
[-0.96602215, -0.93140405],
[-0.90217614, -0.94404832],
[ 1.13747619, 0.95111637],
[ 1.088551 , 0.86479569],
[-1.21400745, -0.90246153],
[-1.23025257, -0.92077401],
[ 1.19250645, 0.96958353],
[-1.10314564, -1.02841596],
[-0.98460503, -0.87206082],
[ 1.03915976, 0.96207912],
[-1.01957207, -0.89147053],
[ 0.9973335 , 1.03344156],
[-0.98515096, -1.13950566],
[ 1.14262977, 1.04566242],
[ 1.06251236, 1.09937002],
[-0.89437865, -0.98460495],
[ 0.95670371, 1.01844879],
[-0.89951709, -0.91685902],
[ 0.95943555, 1.12288485],
[ 0.94825336, 1.02096727],
[ 0.948954 , 0.99463876],
[-1.09823049, -0.99620159],
[ 0.89154527, 1.02907452],
[ 0.98139939, 1.0775685 ],
[ 1.00615056, 0.81981446],
[ 1.08709208, 0.90954863],
[-0.91765909, -1.10070291],
[-1.06392881, -1.03300574],
[-0.75907035, -1.13723942],
[-1.0004216 , -1.05129328]]),
array([-1., -1., -1., 1., -1., 1., 1., 1., -1., -1., -1., -1., -1.,
-1., 1., -1., -1., -1., 1., -1., 1., 1., 1., -1., -1., -1.,
1., 1., 1., 1., 1., -1., -1., 1., -1., -1., -1., -1., -1.,
1., -1., -1., 1., -1., -1., 1., -1., 1., -1., 1., -1., 1.,
-1., -1., -1., -1., 1., 1., -1., -1., -1., 1., -1., 1., 1.,
1., 1., -1., 1., 1., 1., 1., -1., -1., 1., -1., 1., -1.,
-1., -1., 1., 1., -1., 1., 1., 1., -1., 1., -1., 1., -1.,
1., -1., 1., -1., -1., 1., -1., 1., -1., 1., 1., 1., -1.,
-1., 1., -1., 1., -1., 1., 1., -1., 1., -1., 1., -1., -1.,
1., 1., -1., 1., -1., 1., -1., 1., 1., 1., 1., -1., 1.,
-1., -1., -1., 1., -1., 1., 1., 1., 1., -1., -1., 1., -1.,
-1., -1., -1., -1., 1., 1., 1., -1., -1., -1., 1., -1., 1.,
1., 1., 1., 1., -1., -1., 1., 1., 1., 1., 1., 1., 1.,
-1., -1., -1., 1., 1., -1., -1., 1., -1., -1., 1., -1., 1.,
-1., 1., 1., -1., 1., -1., 1., 1., 1., -1., 1., 1., 1.,
1., -1., -1., -1., -1.]))
From rand_tri_gauss
n1 = 20
n2 = 20
n3 = 20
mu1 = [1., 1.]
mu2 = [-1., -1.]
mu3 = [1., -1.]
sigmas1 = [0.9, 0.9]
sigmas2 = [0.9, 0.9]
sigmas3 = [0.9, 0.9]
X2, y2 = rand_tri_gauss(n1, n2, n3, mu1, mu2, mu3, sigmas1, sigmas2, sigmas3)
From rand_clown
n1 = 50
n2 = 50
sigmas1 = 1.
sigmas2 = 5.
X3, y3 = rand_clown(n1, n2, sigmas1, sigmas2)
From rand_checkers
n1 = 150
n2 = 150
sigma = 0.1
X4, y4 = rand_checkers(n1, n2, sigma)
- rand_bi_gauss renvoie un X de 2 classes qui est tiré au hasard parmi deux lois gausssien différentes, et la dernière colonne qui correspond aux labels -1 ou 1.
- rand_tri_gauss renvoie un X de 3 classes qui est tiré au hasard parmi trois lois gaussien différentes, et la dernière colonne qui correspond aux labels 1,2 ou 3.
- rand_clown renvoie un groupe de point gaussien, et un groupe de point selon x_2 = (x_1)^2.
- rand_checkers() point randomsé en 3 groupes
Displaying labeled data
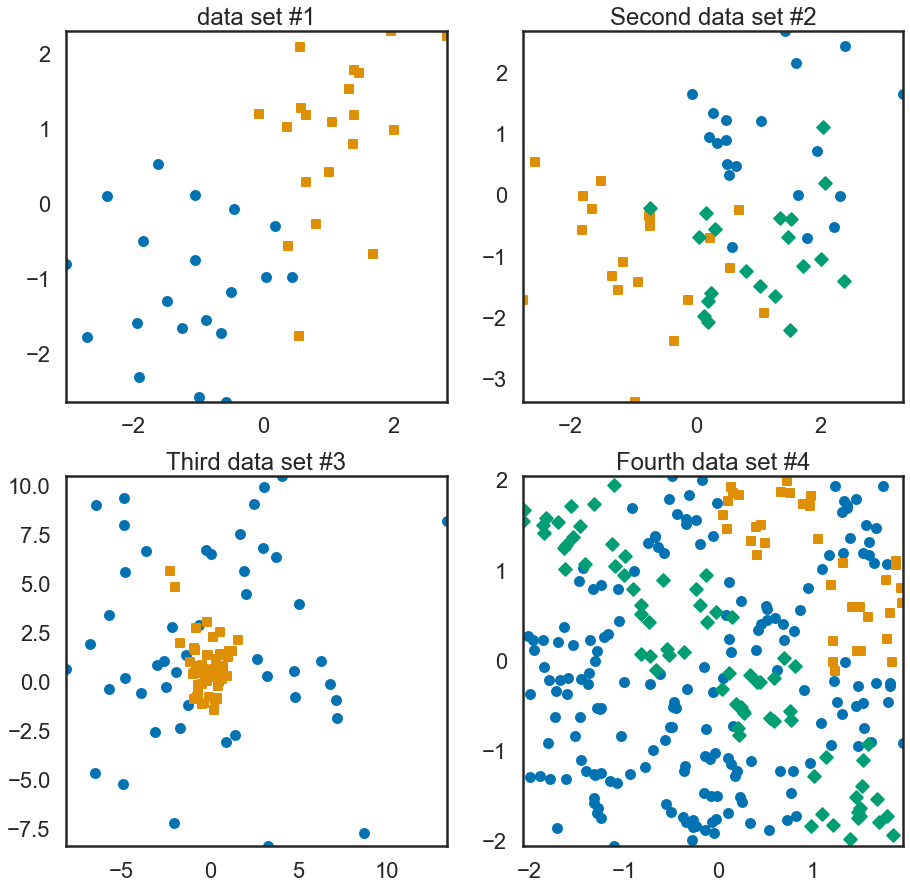
2) Utilisez la fonction plot_2d afin d’afficher les jeux de données générés avec chacune des fonctions.
plt.close("all")
plt.figure(1, figsize=(15, 15))
plt.subplot(221)
plt.title('data set #1')
plot_2d(X1, y1)
plt.subplot(222)
plt.title('Second data set #2')
plot_2d(X2, y2)
plt.subplot(223)
plt.title('Third data set #3')
plot_2d(X3, y3)
plt.subplot(224)
plt.title('Fourth data set #4')
plot_2d(X4, y4)
plt.show()
- La méthode des k-plus proches voisins -

3) Proposez une version adaptée de cette méthode pour la régression, i.e., quand les observations y sont à valeurs réelles : Y = R.
Pour la régression on veut une valeur réelles pour la prédiction, on peut utiliser la moyenne des valeurs d’observation y de K plus proches voisins. On peut aussi ajouter des coefficients (en fonction de distances) sur les valeurs d’observation y pour avoir une moyenne pondérée. eg. Pred = ( Distance * valeur de label )/k
4) Écrivez votre propre classe KNNClassifier avec les méthodes d’apprentissage fit et de classification predict. Choisissez une stratégie de traitement des ex aequo, c’est-à-dire des points avec la même distance ou le même nombre de points de chaque classe dans Vk(x). Vérifier la validité des résultats en les comparant à ceux de la classe KNeighborsClassifier de scikit-learn en utilisant le jeu de données #2. Vous proposerez votre propre méthode de comparaison (par exemple, en utilisant les observations d’indice pair pour le set d’apprentissage et celles d’indice impair pour le set de test). Vous pouvez utilisez le bloc de code si-dessous en complétant le méthodes proposées. Pour plus d’information sur les classes on peut consulter par exemple http://docs.python.org/3/tutorial/ classes.html.
from sklearn.base import BaseEstimator, ClassifierMixin
class KNNClassifier_homemade(BaseEstimator, ClassifierMixin):
""" Homemade kNN classifier class """
def __init__(self, n_neighbors=1):
self.n_neighbors = n_neighbors
pass
def fit(self, X_tr, y_tr):
self.X_tr = X_tr
self.y_tr = y_tr
def predict(self, x):
X = self.X_tr
y = self.y_tr
XSize = X.shape[0]
k = self.n_neighbors
# calcul the distances
diffMat = np.tile(x, (XSize, 1)) - X
sqDiffMat = diffMat**2
sqDistances = sqDiffMat.sum(axis=1)
distances = sqDistances**0.5
# print(diffMat)
# print(distances)
sortedDistIndicies = distances.argsort()
# print(sortedDistIndicies)
# chose the k nearest neighbours and get their label and accumule their distances by label
classCount = {}
# classCount = {label : (count of each label, total distance) }
# 1:(0,0),2:(0,0),3:(0,0)}
for i in range(k):
print(classCount)
voteIlabel = int(y[sortedDistIndicies[i]])
print(voteIlabel)
# count=
classCount[voteIlabel] = (classCount.get(voteIlabel, (0, 0))[
0]+1, classCount.get(voteIlabel, (0, 0))[1]+distances[voteIlabel])
# chose the label the most frequent and si ex aequo chose the class with shortest distance
sortedClassCount = sorted(classCount.items(), key=lambda kv: kv[1],
reverse=True)
# print(classCount.items())
# print(sortedClassCount)
return sortedClassCount[0][0]
Pour le traitement des ex aequo, je calcule les distances totales accumulées de chaque label, s’il y a ex aequo, on choisi celui avec la moindre distance totale.
# test my function
clf = KNNClassifier_homemade(n_neighbors=9)
clf.fit(X2, y2)
clf.predict(np.array([0.70322977, -0.08537583]))
{}
2
{2: (1, 1.4369753038750268)}
1
{2: (1, 1.4369753038750268), 1: (1, 1.3393686423997704)}
1
{2: (1, 1.4369753038750268), 1: (2, 2.6787372847995408)}
3
{2: (1, 1.4369753038750268), 1: (2, 2.6787372847995408), 3: (1, 0.9377028151520462)}
3
{2: (1, 1.4369753038750268), 1: (2, 2.6787372847995408), 3: (2, 1.8754056303040925)}
1
{2: (1, 1.4369753038750268), 1: (3, 4.018105927199311), 3: (2, 1.8754056303040925)}
3
{2: (1, 1.4369753038750268), 1: (3, 4.018105927199311), 3: (3, 2.813108445456139)}
2
{2: (2, 2.8739506077500536), 1: (3, 4.018105927199311), 3: (3, 2.813108445456139)}
1
1
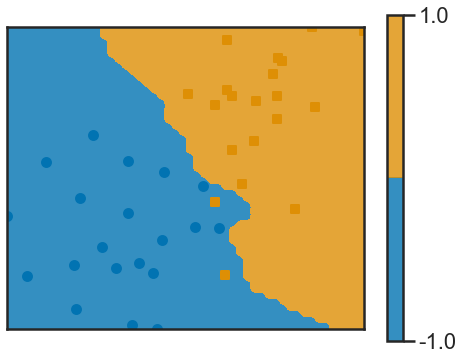
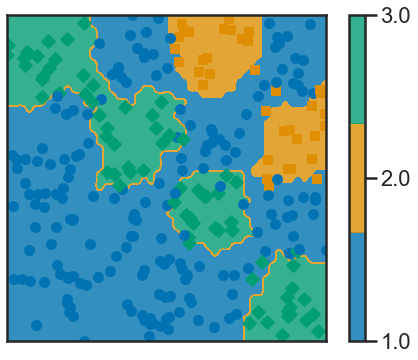
5) Faites tourner sur les quatre exemples de jeu de données cet algorithme de classification, en utilisant la distance euclidienne classique d(x, v) = ∥x − v∥2 et k = 5. Visualisez les règles de classification obtenues en utilisant la fonction frontiere_new. (Souvent, les autres choix de distance peuvent être utiles, par exemple la distance de Mahalanobis.)
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets
n_neighbors = 5
clf = KNeighborsClassifier(n_neighbors=5)
clf.fit(X2, y2)
print(clf.predict([[0.70322977, -0.08537583]]))
[1.]
# k=5
clf.fit(X1, y1)
def f(x): return clf.predict(x.reshape(1, -1))
frontiere_new(f, X1, y1, w=None, step=50, alpha_choice=1,
colorbar=True, samples=True)
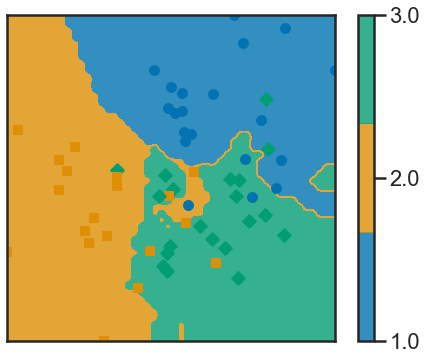
clf = KNeighborsClassifier(n_neighbors=5)
clf.fit(X2, y2)
def f(x): return clf.predict(x.reshape(1, -1))
frontiere_new(f, X2, y2, w=None, step=50, alpha_choice=1, colorbar=True,
samples=True)
clf = KNeighborsClassifier(n_neighbors=5)
clf.fit(X3, y3)
def f(x): return clf.predict(x.reshape(1, -1))
frontiere_new(f, X3, y3, w=None, step=50, alpha_choice=1, colorbar=True,
samples=True)
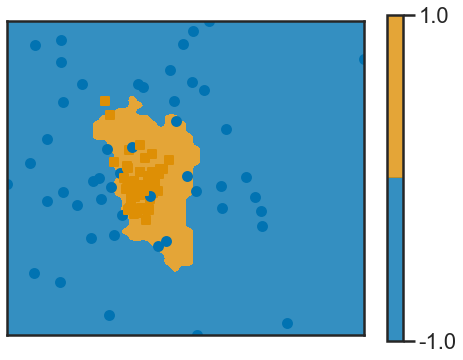
clf = KNeighborsClassifier(n_neighbors=5)
clf.fit(X4, y4)
def f(x): return clf.predict(x.reshape(1, -1))
frontiere_new(f, X4, y4, w=None, step=50, alpha_choice=1, colorbar=True,
samples=True)
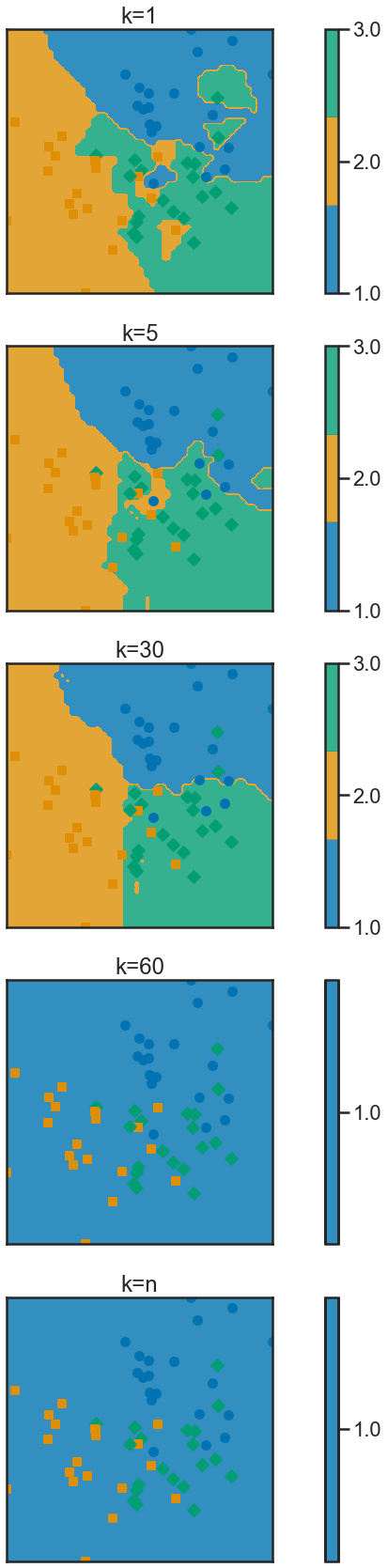
6) Pour les observations d’indice pair du jeu de données #2, faites varier le nombre k de voisins pris en compte : k = 1,2,…,n. Que devient la méthode dans le cas extrême où k = 1? k = n? Afficher ces cas sur les données étudiées en utilisant la fonction frontiere_new et présentez les dans une forme facilement lisible. Dans quels cas la frontière est-elle complexe ? simple ?
- Plus K est grand, plus la frontière est simple. Quand k = 1, il va faire beaucoup d’enclave. Quand k = n, il n’y plus de frontière cars tous les points sont dans la même class.
knn0 = KNeighborsClassifier(n_neighbors=5)
knn0 = knn0.fit(X2, y2)
knn1 = KNeighborsClassifier(n_neighbors=30)
knn1 = knn1.fit(X2, y2)
knn2 = KNeighborsClassifier(n_neighbors=60)
knn2 = knn2.fit(X2, y2)
knn3 = KNeighborsClassifier(n_neighbors=len(X2))
knn3 = knn3.fit(X2, y2)
knn4 = KNeighborsClassifier(n_neighbors=1)
knn4 = knn4.fit(X2, y2)
plt.figure(num=None, figsize=(20, 30))
# k=1
plt.subplot(511)
plt.title("k=1")
def f(x): return knn4.predict(x.reshape(1, -1))
frontiere_new(f, X=X2, y=y2)
# k=5
plt.subplot(512)
plt.title("k=5")
def f(x): return knn0.predict(x.reshape(1, -1))
frontiere_new(f, X=X2, y=y2)
# k=30
plt.subplot(513)
plt.title("k=30")
def f(x): return knn1.predict(x.reshape(1, -1))
frontiere_new(f, X=X2, y=y2)
# k=60
plt.subplot(514)
plt.title("k=60")
def f(x): return knn2.predict(x.reshape(1, -1))
frontiere_new(f, X=X2, y=y2)
# k=n
plt.subplot(515)
plt.title("k=n")
def f(x): return knn3.predict(x.reshape(1, -1))
frontiere_new(f, X=X2, y=y2)
Q7 Une variante possible très utilisée consiste à pondérer les poids du $j$-ème voisin selon $e^{−d^2_j/h}$ ($h$ contrôlant le niveau de pondération) : cela revient à remplacer l’Équation (2) par :
Implémentez cette variante dans scikit-learn en passant le paramètre weights au constructeurde KNeighborsClassifier. (Une autre possibilité consiste à pondérer les variables et non seulement les observations, on le regarde pas ici.) On pourra s’inspirer de _weight_func de la partie test de scikit-learn : https://github.com/scikit-learn/scikit-learn/blob/master/sklearn/neighbors/tests/test_neighbors.py Pour tester l’impact du choix de $h$ sur les frontières de classification, visualisez les règles de classification pour $k = 7$ et $h = 10^j$ avec $j = −2, −1, 0, 1, 2$ ; utilisez les observations d’indice pair du jeux de données #2 pour l’entrainement du classifieur (Vous pouvez utiliser la fonction frontiere_new.)
def weight_func(dist):
""" Weight function to replace lambda d: d ** -2.
The lambda function is not valid because:
if d==0 then 0^-2 is not valid. """
# Dist could be multidimensional, flatten it so all values
# can be looped
h = 10**(-j)
weight = np.exp((-(dist**2)/h))
#print(j,h,weight,dist)
return weight
"""# my first methode to split
train = []
i = 0
while i < len(X2):
train.append(i)
i = i+2"""
plt.figure(num=None, figsize=(20, 30))
j = -2
knn = KNeighborsClassifier(n_neighbors=7, weights=weight_func)
knn0 = knn.fit(X2[::2], y2[::2])
plt.subplot(511)
plt.title("j=-2")
def f(x): return knn0.predict(x.reshape(1, -1))
frontiere_new(f, X=X2[::2], y=y2[::2])
j = -1
knn = KNeighborsClassifier(n_neighbors=7, weights=weight_func)
knn1 = knn.fit(X2[::2], y2[::2])
plt.subplot(512)
plt.title("j=-1")
def f(x): return knn1.predict(x.reshape(1, -1))
frontiere_new(f, X=X2[::2], y=y2[::2])
j = 0
knn2 = KNeighborsClassifier(n_neighbors=7, weights=weight_func)
knn2 = knn.fit(X2[::2], y2[::2])
plt.subplot(513)
plt.title("j=0")
def f(x): return knn2.predict(x.reshape(1, -1))
frontiere_new(f, X=X2[::2], y=y2[::2])
j = 1
knn3 = KNeighborsClassifier(n_neighbors=7, weights=weight_func)
knn3 = knn3.fit(X2[::2], y2[::2])
plt.subplot(514)
plt.title("j=1")
def f(x): return knn3.predict(x.reshape(1, -1))
frontiere_new(f, X=X2[::2], y=y2[::2])
j = 2
knn4 = KNeighborsClassifier(n_neighbors=7, weights=weight_func)
knn4 = knn4.fit(X2[::2], y2[::2])
plt.subplot(515)
plt.title("j=2")
def f(x): return knn4.predict(x.reshape(1, -1))
frontiere_new(f, X=X2[::2], y=y2[::2])
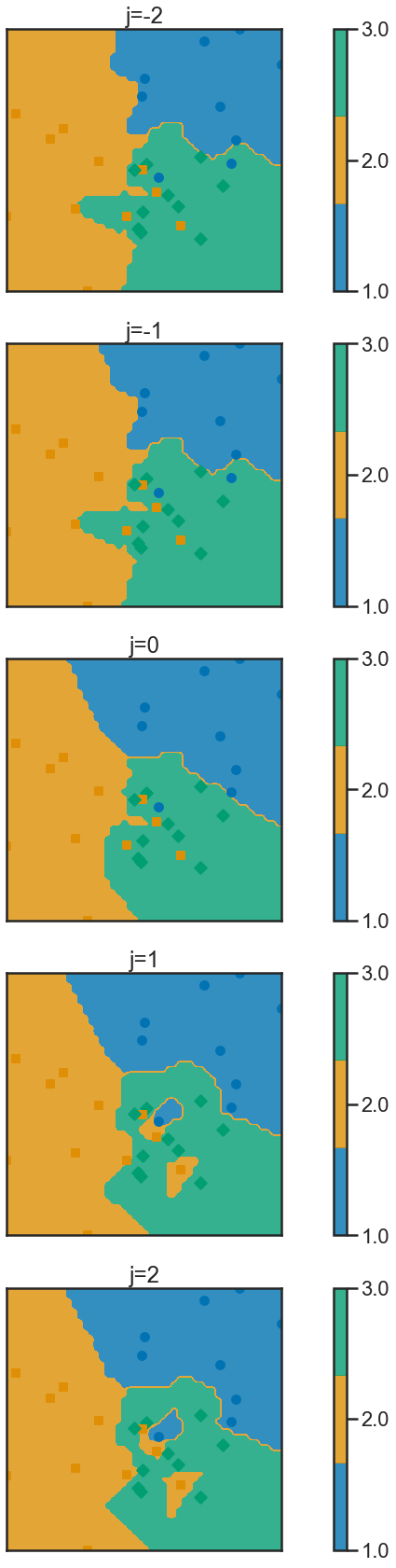
- Plus h est grand, plus les voisins proches deviennent important, la classification est influencé par les voisins les plus proches, la frontière devient plus complexe (Elle devient plus lisse par endroit mais a tendance à créer plus d’enclave).
8) Quel est le taux d’erreur sur les mêmes données d’apprentissage (i.e., la proportion d’erreur faite par le classifieur) lorsque k = 1 ? et sur des données de test (les observations d’indice pair) ?
knn8 = KNeighborsClassifier(n_neighbors=1)
knn8 = knn8.fit(X2[::2], y2[::2])
pred = knn8.predict(X2[::2])
print("Le taux d'erreur sur les mêmes données d’apprentissage est de:", round(
(1 - accuracy_score(pred, y2[::2]))*100, 2), "%")
pred = knn8.predict(X2[1::2])
print("Le taux d'erreur sur des données de test est de:", round(
(1 - accuracy_score(pred, y2[1::2]))*100, 2), "%")
Le taux d'erreur sur les mêmes données d’apprentissage est de: 0.0 %
Le taux d'erreur sur des données de test est de: 23.33 %
Le taux d’erreur sur les mêmes données d’apprentissage est de: 0.0 %. C’est à dire le risque empirique sur les mêmes données d’apprentissage est 0, mais le risque de generalisation est grand. Le model avec k=1 est clairement overfitted, la capacité de généralisation est mauvaise.
9) Pour le jeu de données #4, en utilisant les observations d’indice pair pour l’apprentissage et les ob- servations d’indice impair pour le test, tracez le taux d’erreur en fonction de k pour k = 1, 2, . . . , 50. Vous pourrez utiliser la classe fournie ErrorCurve.
from sklearn.metrics import accuracy_score
knn8 = KNeighborsClassifier(n_neighbors=1)
knn8 = knn8.fit(X4[::2], y4[::2])
pred = knn8.predict(X4[1::2])
print("Le taux d'erreur est de:", round(
(1 - accuracy_score(pred, y4[1::2]))*100, 2), "%")
Le taux d'erreur est de: 14.58 %
curve = ErrorCurve(k_range=list(range(1, 50)))
ErrorCurve.fit_curve(curve, X4[::2], y4[::2], X4[1::2], y4[1::2])
ErrorCurve.plot(curve)
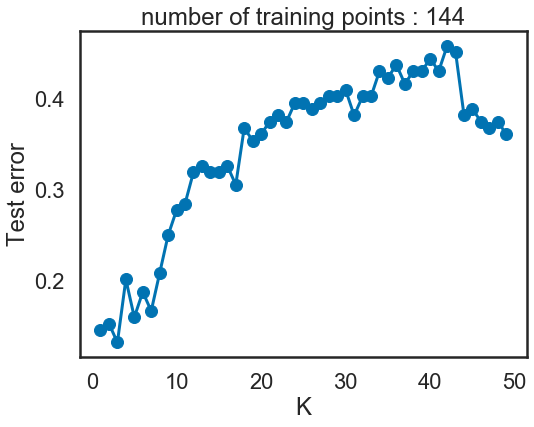
- Quand k est proche de 1, le modèle est overfitted;
- quand le k est proche de n, le modèle n’apprends pas des informations sur les données, on a le problème de underfitting.
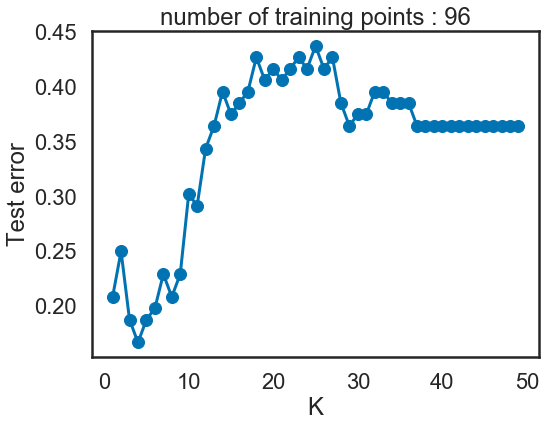
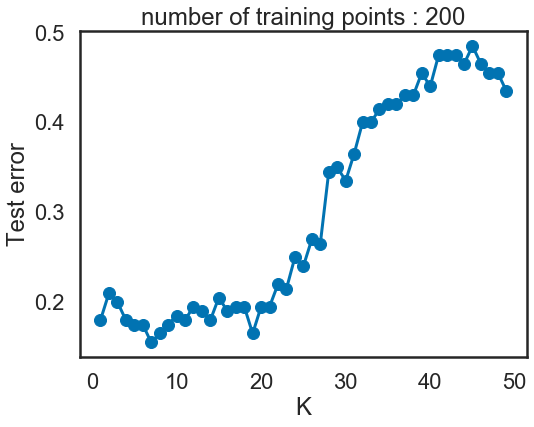
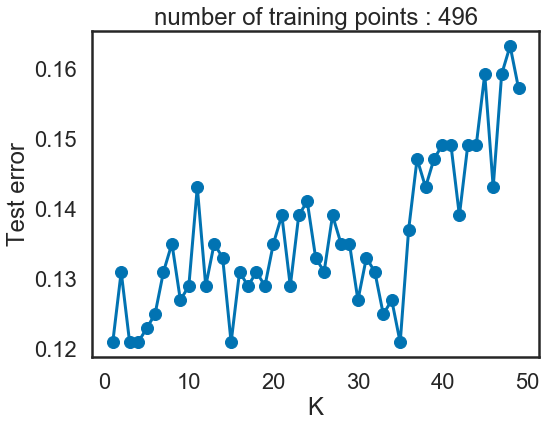
10) Tracez les différentes courbes d’erreur en fonction du paramètre k = (1,2,…,50) sur le jeu de données #4, pour des nombres d’échantillons d’entrainement n prenant les valeurs 100, 200, 500 à 1000. Cette fois, tirez l’ensemble d’apprentissage et l’ensemble de test indépendamment et de même taille. Quelle est la meilleure valeur de k ? Est-ce la même pour les différents datasets ? Vous pourrez utiliser la classe fournie ErrorCurve. Pour n = 1000 visualisez les données et la règle de décision sur le même graphique. (Vous pouvez utiliser la fonction frontiere_new.)
i = 100
X4_10, y4_10 = rand_checkers(i, i, 0.1)
curve = ErrorCurve(k_range=list(range(1, 50)))
curve.fit_curve(X4_10[::2], y4_10[::2], X4_10[1::2], y4_10[1::2])
ErrorCurve.plot(curve)
i = 200
X4_10, y4_10 = rand_checkers(i, i, 0.1)
curve = ErrorCurve(k_range=list(range(1, 50)))
curve.fit_curve(X4_10[::2], y4_10[::2], X4_10[1::2], y4_10[1::2])
ErrorCurve.plot(curve)
i = 500
X4_10, y4_10 = rand_checkers(i, i, 0.1)
curve = ErrorCurve(k_range=list(range(1, 50)))
curve.fit_curve(X4_10[::2], y4_10[::2], X4_10[1::2], y4_10[1::2])
ErrorCurve.plot(curve)
i = 1000
X4_10, y4_10 = rand_checkers(i, i, 0.1)
curve = ErrorCurve(k_range=list(range(1, 50)))
curve.fit_curve(X4_10[::2], y4_10[::2], X4_10[1::2], y4_10[1::2])
ErrorCurve.plot(curve)
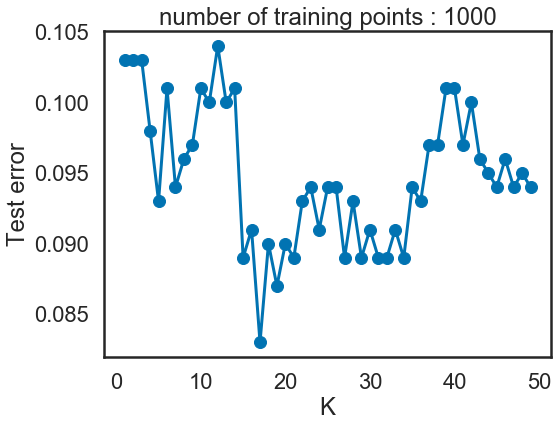
- Quand test data = 100 or 200, quand k est proche de 1, le modèle est overfitted; quand le k est proche de 50, le modèle n’apprends pas des informations sur les données, on a le problème de underfitting.
- Quand test data = 500 or 1000, on a beacoup de points, c’est à dire ce modèle génératif KNN contient beaucoup d’information. En même temps, comme on a beaucoup de points, même si k = 50, les 50 plus proches voisins sont très proches et regroupés. 50 est petit par rapport 1000 points , il n’y a pas de problème d’underfitting. D’où le très bon performance quand test data = 500 or 1000.
11) A votre avis, quels sont les avantages et les inconvénients de la méthode des plus proches voisins : temps de calcul ? passage à l’échelle ? interprétabilité ?
- La méthode des plus proches voisions doit parcourir tout l’espace X, donc la KNN subit le fléau de la dimension, et est particulièrement gourmand en termes de temps de calcul. Le passage à l’échelle est donc complexe. Cependant la KNN est facile à interpréter et efficiente si le nombre de dimensions est relativement faible.
12) Étudiez la base digits de scikit-learn. On pourra se référer à http://scikit-learn.org/stable/ _downloads/plot_digits_classification.py pour le chargement et la manipulation de la base de données. Pour de plus amples informations sur la nature de la classe ‘Bunch’ (une sous-classe de dictionnaire, on se reportera à la documentation sur la classe ‘dict’ : http://docs.python.org/ 2/library/stdtypes.html#mapping-types-dict. Décrivez la nature et le format des données (précisément), affichez un exemple. Tracez l’histogramme pour des classes. Coupez l’échantillon en deux parties de même taille et utilisez la première partie pour l’apprentissage et la deuxième pour le test. Appliquez la méthode aux données issues de la base digits pour un choix de k ≥ 1 (e.g., k = 30) et indiquez le taux d’erreur.
- Bunch: Dictionary-like object, the interesting attributes are: ‘data’, the data to learn, ‘images’, the images corresponding to each sample, ‘target’, the classification labels for each sample, ‘target_names’, the meaning of the labels, and ‘DESCR’, the full description of the dataset.
La variable digits contient un dictionnaire composé des clefs suivantes:
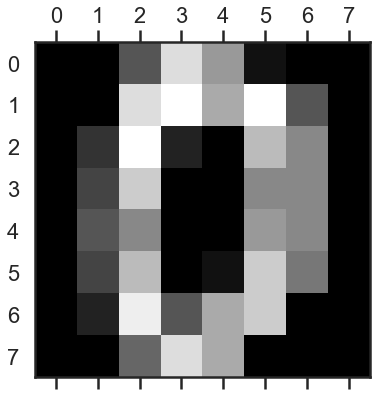
- images: Elle contient un array composé d’images. Ces images sont elles meme des arrays 2D contentanant chacun 8 listes de 8 entiers. Ce sont l’intensité de noir (de 0 à 16) dans les 8 rangés de 8 pixels qui forment notre image
- ‘data’: La meme data que la clefs images, mais flattened. C’est donc un un array contenant les intensites de pixel des images mais flattened; dans un array 1D de 8*8=64 cases.
- ‘target_names’: La valeur des differentes classes
- ‘target’: Un array d’indexes correspondants aux classes associés à ce meme index dans les arrays image/data
Each datapoint is a 8x8 image of a digit.
Classes 10 Samples per class ~180 Samples total 1797 Dimensionality 64 Features integers 0-16
from sklearn.datasets import load_digits
digits = load_digits()
print(digits.data.shape)
import matplotlib.pyplot as plt
plt.gray()
plt.matshow(digits.images[0])
plt.show()
(1797, 64)
<Figure size 576x432 with 0 Axes>
digits.DESCR
".. _digits_dataset:\n\nOptical recognition of handwritten digits dataset\n--------------------------------------------------\n\n**Data Set Characteristics:**\n\n :Number of Instances: 5620\n :Number of Attributes: 64\n :Attribute Information: 8x8 image of integer pixels in the range 0..16.\n :Missing Attribute Values: None\n :Creator: E. Alpaydin (alpaydin '@' boun.edu.tr)\n :Date: July; 1998\n\nThis is a copy of the test set of the UCI ML hand-written digits datasets\nhttps://archive.ics.uci.edu/ml/datasets/Optical+Recognition+of+Handwritten+Digits\n\nThe data set contains images of hand-written digits: 10 classes where\neach class refers to a digit.\n\nPreprocessing programs made available by NIST were used to extract\nnormalized bitmaps of handwritten digits from a preprinted form. From a\ntotal of 43 people, 30 contributed to the training set and different 13\nto the test set. 32x32 bitmaps are divided into nonoverlapping blocks of\n4x4 and the number of on pixels are counted in each block. This generates\nan input matrix of 8x8 where each element is an integer in the range\n0..16. This reduces dimensionality and gives invariance to small\ndistortions.\n\nFor info on NIST preprocessing routines, see M. D. Garris, J. L. Blue, G.\nT. Candela, D. L. Dimmick, J. Geist, P. J. Grother, S. A. Janet, and C.\nL. Wilson, NIST Form-Based Handprint Recognition System, NISTIR 5469,\n1994.\n\n.. topic:: References\n\n - C. Kaynak (1995) Methods of Combining Multiple Classifiers and Their\n Applications to Handwritten Digit Recognition, MSc Thesis, Institute of\n Graduate Studies in Science and Engineering, Bogazici University.\n - E. Alpaydin, C. Kaynak (1998) Cascading Classifiers, Kybernetika.\n - Ken Tang and Ponnuthurai N. Suganthan and Xi Yao and A. Kai Qin.\n Linear dimensionalityreduction using relevance weighted LDA. School of\n Electrical and Electronic Engineering Nanyang Technological University.\n 2005.\n - Claudio Gentile. A New Approximate Maximal Margin Classification\n Algorithm. NIPS. 2000."
digits.data
array([[ 0., 0., 5., ..., 0., 0., 0.],
[ 0., 0., 0., ..., 10., 0., 0.],
[ 0., 0., 0., ..., 16., 9., 0.],
...,
[ 0., 0., 1., ..., 6., 0., 0.],
[ 0., 0., 2., ..., 12., 0., 0.],
[ 0., 0., 10., ..., 12., 1., 0.]])
digits.images
array([[[ 0., 0., 5., ..., 1., 0., 0.],
[ 0., 0., 13., ..., 15., 5., 0.],
[ 0., 3., 15., ..., 11., 8., 0.],
...,
[ 0., 4., 11., ..., 12., 7., 0.],
[ 0., 2., 14., ..., 12., 0., 0.],
[ 0., 0., 6., ..., 0., 0., 0.]],
[[ 0., 0., 0., ..., 5., 0., 0.],
[ 0., 0., 0., ..., 9., 0., 0.],
[ 0., 0., 3., ..., 6., 0., 0.],
...,
[ 0., 0., 1., ..., 6., 0., 0.],
[ 0., 0., 1., ..., 6., 0., 0.],
[ 0., 0., 0., ..., 10., 0., 0.]],
[[ 0., 0., 0., ..., 12., 0., 0.],
[ 0., 0., 3., ..., 14., 0., 0.],
[ 0., 0., 8., ..., 16., 0., 0.],
...,
[ 0., 9., 16., ..., 0., 0., 0.],
[ 0., 3., 13., ..., 11., 5., 0.],
[ 0., 0., 0., ..., 16., 9., 0.]],
...,
[[ 0., 0., 1., ..., 1., 0., 0.],
[ 0., 0., 13., ..., 2., 1., 0.],
[ 0., 0., 16., ..., 16., 5., 0.],
...,
[ 0., 0., 16., ..., 15., 0., 0.],
[ 0., 0., 15., ..., 16., 0., 0.],
[ 0., 0., 2., ..., 6., 0., 0.]],
[[ 0., 0., 2., ..., 0., 0., 0.],
[ 0., 0., 14., ..., 15., 1., 0.],
[ 0., 4., 16., ..., 16., 7., 0.],
...,
[ 0., 0., 0., ..., 16., 2., 0.],
[ 0., 0., 4., ..., 16., 2., 0.],
[ 0., 0., 5., ..., 12., 0., 0.]],
[[ 0., 0., 10., ..., 1., 0., 0.],
[ 0., 2., 16., ..., 1., 0., 0.],
[ 0., 0., 15., ..., 15., 0., 0.],
...,
[ 0., 4., 16., ..., 16., 6., 0.],
[ 0., 8., 16., ..., 16., 8., 0.],
[ 0., 1., 8., ..., 12., 1., 0.]]])
digits.target
array([0, 1, 2, ..., 8, 9, 8])
digits.target_names
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
images_and_labels = list(zip(digits.images, digits.target))
for index, (image, label) in enumerate(images_and_labels[:4]):
plt.subplot(2, 4, index + 1)
plt.axis('off')
plt.imshow(image)
plt.title('image: %i' % label)

for index, (image, label) in enumerate(images_and_labels[:100]):
plt.subplot(10, 10, index + 1)
plt.axis('off')
plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')

from sklearn import metrics
def split_data(X, y):
return [
X[::2],
y[::2],
X[1::2],
y[1::2],
]
X_train, y_train, X_test, y_test = split_data(digits.data, digits.target)
knn = KNeighborsClassifier(n_neighbors=30).fit(X_train, y_train)
y_pred = knn.predict(X_test)
print("Number of elements in test sample:", len(y_test))
print("Errors rate:", 1-accuracy_score(y_pred, y_test))
print((metrics.classification_report(y_test, knn.predict(X_test))))
Number of elements in test sample: 898
Errors rate: 0.055679287305122505
precision recall f1-score support
0 0.99 1.00 0.99 88
1 0.89 0.99 0.94 89
2 0.97 0.92 0.94 91
3 0.99 0.91 0.95 93
4 0.95 0.99 0.97 88
5 0.95 0.96 0.95 91
6 0.97 1.00 0.98 90
7 0.91 1.00 0.95 91
8 0.89 0.87 0.88 86
9 0.96 0.80 0.87 91
accuracy 0.94 898
macro avg 0.95 0.94 0.94 898
weighted avg 0.95 0.94 0.94 898
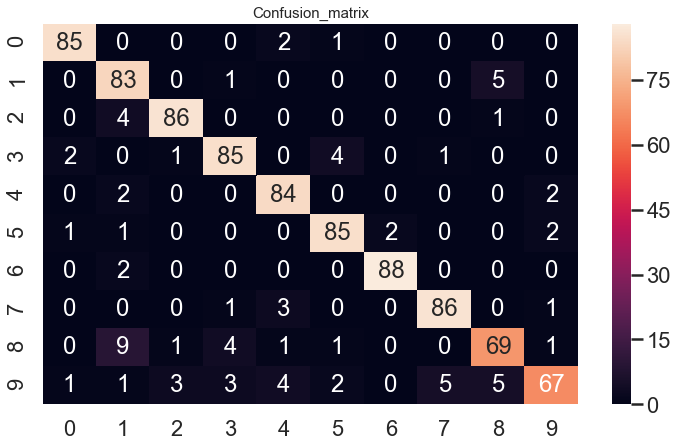
13) Estimez la matrice de confusion $(\mathbb{P}{Y = i, C_k(X) = j})_{i, j}$ associée au classifieur $C_k$ ainsi obtenu et visualisez celle-ci. Pour la manipulation de telles matrices avec scikit-learn, on pourra consulter http://scikit-learn.org/stable/auto_examples/model_selection/plot_confusion_matrix.html.
plt.figure(figsize=(12, 7))
sns.heatmap(metrics.confusion_matrix(
y_test, y_pred), annot=True, fmt='3.0f')
plt.title('Confusion_matrix', y=1.05, size=15)
Text(0.5, 1.05, 'Confusion_matrix')
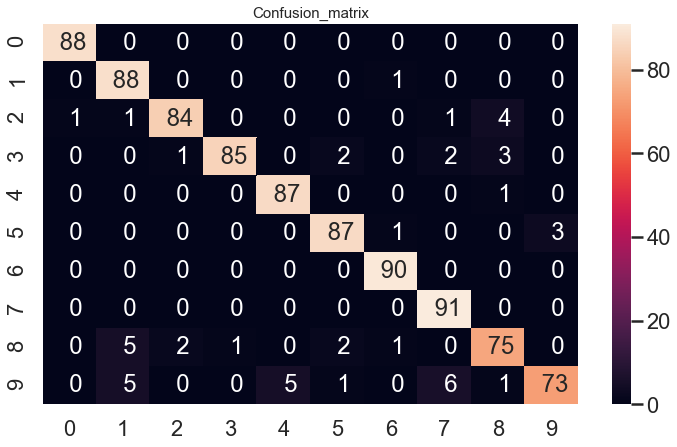
- On voit que le classifieur se trompe parfois 1 pour 8, 9. Mais il n’affiche pas le pourcentage.
14) Proposez une méthode pour choisir k et mettez-la en œuvre. Vous pourrez utiliser la classe fournie LOOCurve. En utilisant toutes les données, tracez la courbe du taux d’erreur leave-one-out pour k = 1, 6, 11, 16, 21, 26, 31, 36, 41, 46, 100, 200. Pour plus d’information sur la validation croisée (cross- validation) on peut consulter [HTF09, Chapitre 7.10].
k14 = [1, 6, 11, 16, 21, 26, 31, 36, 41, 46, 100, 200]
loo = LOOCurve(k_range=k14)
loo.fit_curve(digits.data, digits.target)
loo.plot()
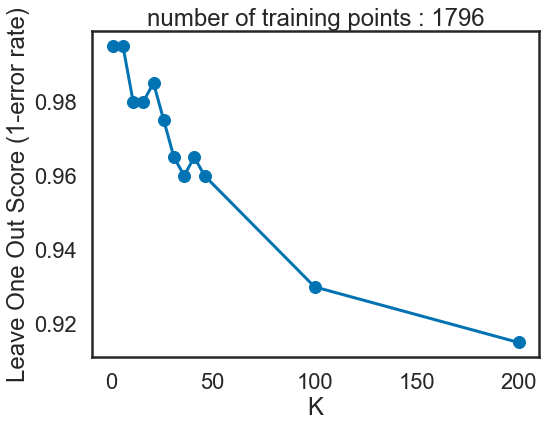
avec LOOCV on a trouvé le meilleur k = 6 (k =1 est overfitted).
# Another way to find the best k
from sklearn.model_selection import GridSearchCV
knn = KNeighborsClassifier()
knn_param_grid = {"n_neighbors": [6, 11, 16, 21, 26, 31, 36, 41, 46, 100, 200]}
knnCV = GridSearchCV(knn, param_grid=knn_param_grid, cv=10,
scoring="accuracy", n_jobs=-1, verbose=1)
knnCV.fit(digits.data, digits.target)
# Best param
param_knnCV = knnCV.best_estimator_
result_knnCV = knnCV.best_score_*100
print("Accuracy CV : %.2f%% ", (result_knnCV))
Fitting 10 folds for each of 11 candidates, totalling 110 fits
[Parallel(n_jobs=-1)]: Using backend LokyBackend with 4 concurrent workers.
[Parallel(n_jobs=-1)]: Done 42 tasks | elapsed: 5.3s
Accuracy CV : %.2f%% 96.93934335002783
[Parallel(n_jobs=-1)]: Done 110 out of 110 | elapsed: 8.8s finished
# the best k found is 6 (after 1)
param_knnCV
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=6, p=2,
weights='uniform')
Avec la méthode de Cross Validation en utilisant GridSearchCV, on a trouvé le meilleur k = 6 . C’est le même résultat que LOOCurve
Pour aller plus loin -
Des détails généraux sur la méthode des k-plus proches voisins se trouvent dans [HTF09, Chapitre 13]. Pour améliorer la compréhension théorique de la méthode on peut se reporter au livre [DGL96, Chapitre 11] et les limites de la méthode quand k = 1 http://certis.enpc.fr/%7Edalalyan/Download/DM1.pdf. Enfin pour les considérations algorithmiques on pourra commencer par lire http://scikit-learn.org/ stable/modules/neighbors.html#brute-force et les paragraphes suivants.
Le nom anglais est Linear Discirmiant Analysis (LDA). Il est préférable de se reporter à cette dénomi- nation en vue de trouver de l’aide en ligne pour la partie numérique. Attention toutefois à ne pas confondre avec Latent Dirichlet Allocation qui est un modèle statistique hiérarchique pour données catégorielles et qui n’a pas de lien avec l’Analyse Discriminante Linéaire.

15)
Donc: On a aussi:
16)
log-ratio: avec (7)(8) on a et
donc
17)
Pour le classifier predict 1, on a alors on a donc d’où et sinon notre LDA predict -1.
Mise en oeuvre
18) Écrivez votre propre classe LDAClassifier avec les méthodes d’apprentissage fit et de classification predict.
from sklearn.base import BaseEstimator, ClassifierMixin
import numpy as np
class LDAClassifier_Homemade(BaseEstimator, ClassifierMixin):
""" Homemade LDA classifier class """
def __init__(self):
pass
def fit(self, X_tr, y_tr):
# m= num of y_tr=1
# n= num of y_tr
y = y_tr
X = X_tr
m = np.sum(y[y == 1])
n = y.shape[0]
self.pi_positif = m/n
# calcul Pi+ , mu+, mu-, sigma(variance)
# numpy.where(condition[, x, y])
# Return elements chosen from x or y depending on condition.
mu_positif = np.sum(X_tr[np.where(y == 1), :][0], axis=0).T/m
mu_negatif = np.sum(X_tr[np.where(y == -1), :][0], axis=0).T/(n-m)
# variance
sigma_positif = np.dot((X[np.where(y == 1), :][0] - mu_positif.T).T,
(X[np.where(y == 1), :][0] - mu_positif.T)) / (m-1)
sigma_negatif = np.dot((X[np.where(y == -1), :][0]-mu_negatif.T).T,
(X[np.where(y == -1), :][0]-mu_negatif.T)) / (n-m-1)
sigma = ((m-1)*sigma_positif+(n-m-1)*sigma_negatif)/(n-2)
self.mu_positif = mu_positif
self.mu_negatif = mu_negatif
self.sigma = sigma
self.m = m
self.n = n
return self
def predict(self, X):
# We use the mu, sigma calculated in fit()
mu_positif = self.mu_positif
mu_negatif = self.mu_negatif
sigma = self.sigma
m = self.m
n = self.n
pred = []
# for each point in X, we predict its label
for x in X:
#print(np.dot(np.dot(x, np.linalg.inv(sigma)), (mu_positif-mu_negatif)))
# print(1/2*np.dot(np.dot(mu_positif, np.linalg.inv(sigma)), mu_positif.T) - \
# 1/2*np.dot(np.dot(mu_negatif, np.linalg.inv(sigma)), mu_negatif.T) \
# + np.log(1-m/n) - np.log(m/n))
# both ends have negative values
if np.dot(
np.dot(x, np.linalg.inv(sigma)), (mu_positif-mu_negatif)) \
> 1/2*np.dot(np.dot(mu_positif, np.linalg.inv(sigma)), mu_positif.T) - \
1/2*np.dot(np.dot(mu_negatif, np.linalg.inv(sigma)), mu_negatif.T) \
+ np.log(1-m/n) - np.log(m/n):
pred.append(1)
else:
pred.append(-1)
return pred
- On applique l’inégalité obtenu dans la question 17.
LDA = LDAClassifier_Homemade().fit(X1, y1)
y_pred = LDA.predict(X1)
19) Importez le module sklearn.discriminant_analysis qui contient en particulier la classe LinearDiscriminantAnalysis qui nous servira dans la suite.
Vérifiez la validité des résultats obtenus avec votre méthode en les comparant à ceux de la classe LinearDiscriminantAnalysis de scikit-learn en utilisant un jeu de données simulé. Vous propo- serez votre propre méthode de comparaison (l’échantillon d’apprentissage doit être petit et l’échan- tillon de validation doit être assez grand ; on considère par ailleurs que m est différent de n − m, i.e., les deux classes ne sont pas représentées par le même nombre d’échantillons observés). Indiquez les taux d’erreur de LDAClassifier et de LinearDiscriminantAnalysis et le nombre de cas où les prédictions coïncident. En utilisant votre classe LDAClassifier, visualisez la règle de classification. (Vous pouvez utiliser la fonction frontiere_new.)
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.model_selection import train_test_split
#un jeu de données simulé. m est différent de n − m
X1, y1 = rand_bi_gauss(1450, 390, [0,1], [0,1.1], [0.1,0.1], [0.1,0.1])
#Echantillon de validation relativement grand
X_1_train,X_1_test,y_1_train,y_1_test = train_test_split(X1,y1,test_size=0.8,random_state=1)
lda_homemade= LDAClassifier_Homemade()
lda_homemade.fit(X_1_train,y_1_train)
lda_homemade_pred = lda_homemade.predict(X_1_test)
result = accuracy_score(y_1_test, lda_homemade_pred)*100
print(" lda_homemade Model Accuracy " , result, "%")
lda_homemade Model Accuracy 78.73641304347827 %
lda= LinearDiscriminantAnalysis()
lda.fit(X_1_train,y_1_train)
y_pred_lda=lda.predict(X_1_test)
result = accuracy_score(y_1_test, y_pred_lda)*100
print(" lda_homemade Model Accuracy : " , result, "%")
lda_homemade Model Accuracy : 78.73641304347827 %
Même quand je fais exprès de tester sur les points très proches,Le LDA Homemade donne le même résultat que LinearDiscriminantAnalysis de Scikit-learn.
def f(x): return lda.predict(x.reshape(1, -1))
frontiere_new(f, X1, y1, w=None, step=50, alpha_choice=1, colorbar=True,samples=True)
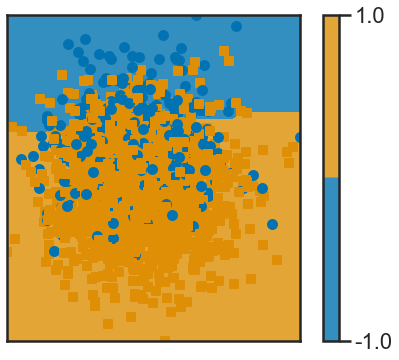
# un jeu de données simulé. m est différent de n − m
X1, y1 = rand_bi_gauss(1450, 390, [0, 1], [1, 2], [0.25, 0.25], [0.1, 0.1])
# Echantillon de validation relativement grand
X_1_train, X_1_test, y_1_train, y_1_test = train_test_split(
X1, y1, test_size=0.8, random_state=1)
lda_homemade = LDAClassifier_Homemade()
lda_homemade.fit(X_1_train, y_1_train)
lda_homemade_pred = lda_homemade.predict(X_1_test)
result = accuracy_score(y_1_test, lda_homemade_pred)*100
print(" lda_homemade Model Accuracy ", result, "%")
lda = LinearDiscriminantAnalysis()
lda.fit(X_1_train, y_1_train)
y_pred_lda = lda.predict(X_1_test)
result = accuracy_score(y_1_test, y_pred_lda)*100
print(" lda_homemade Model Accuracy : ", result, "%")
lda_homemade Model Accuracy 99.93206521739131 %
lda_homemade Model Accuracy : 99.93206521739131 %
Le LDA Homemade donne le même résultat que LinearDiscriminantAnalysis de Scikit-learn. Même resultat quand on fait exprès de tester sur les points très proches.
def f(x): return lda_homemade.predict(x.reshape(1, -1))
frontiere_new(f, X1, y1, w=None, step=50, alpha_choice=1,
colorbar=True, samples=True)
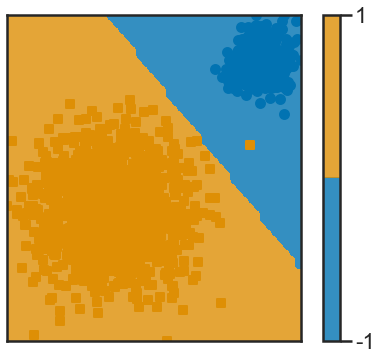
* LDA a trouver un hyperplan qui maximise la distance vers mu+ et mu-, en tenant consideration des variances de chaque classe.
20)En utilisant votre classe LDAClassifier, visualisez la règle de classification pour les jeux de données #1 et #3. (Vous pouvez utiliser la fonction frontiere_new.) Discutez l’efficacité de la méthode dans ces deux cas.
# un jeu de données simulé. m est différent de n − m
X1, y1 = rand_bi_gauss(1450, 390, [0, 1], [1, 2], [0.1, 0.1], [0.1, 0.1])
lda_homemade = LDAClassifier_Homemade()
lda_homemade.fit(X1, y1)
def f(x): return lda_homemade.predict(x.reshape(1, -1))
frontiere_new(f, X1, y1, w=None, step=50, alpha_choice=1,
colorbar=True, samples=True)

LDA est un classifier linéaire, il marche très bien sur le jeux de données linéairement séparable.
n1 = 50
n2 = 50
sigmas1 = 5
sigmas2 = 5
X3, y3 = rand_clown(n1, n2, sigmas1, sigmas2)
def f(x): return lda_homemade.predict(x.reshape(1, -1))
frontiere_new(f, X3, y3, w=None, step=50, alpha_choice=1,
colorbar=True, samples=True)
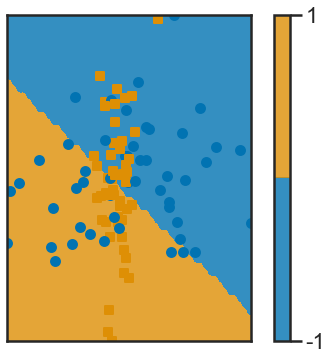
LDA est un classifier linéaire, il marche pas très bien sur le jeux de données #3 qui n’est pas linéairement séparable, il faudra envisager des méthodes non linéaires ou kernel tricks.
Régression logistique -
Méthode discriminative avec régression logistique
Importer le module sklearn.linear_model qui contient en particulier la classe LogisticRegression qui nous servira dans la suite.
21) Appliquez la classification par régression logistique sur les données rand_bi_gauss. Comparer les résultats avec la LDA, notamment lorsque une classe est beaucoup plus petite que l’autre (a beaucoup moins d’observations). On parle alors de classes déséquilibrées.
# un jeu de données simulé. (y+ y-) class déséquilibrées
X1, y1 = rand_bi_gauss(250, 10, [0, 1], [1, 2], [0.25, 0.25], [0.25, 0.25])
# 20% training data %80 test data avec stratification
X_1_train, X_1_test, y_1_train, y_1_test = train_test_split(
X1, y1, test_size=0.8, random_state=1, stratify=y1)
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(solver='liblinear', C=1e9)
lr.fit(X_1_train, y_1_train)
y_pred_lr = lr.predict(X_1_test)
result_lr = accuracy_score(y_1_test, y_pred_lr)*100
print("Logistic Regression Model Accuracy: ", result_lr, "%")
Logistic Regression Model Accuracy: 99.51923076923077 %
lda = LinearDiscriminantAnalysis()
lda.fit(X1, y1)
y_pred_lr = lda.predict(X_1_test)
result_lr = accuracy_score(y_1_test, y_pred_lr)*100
print("LDA Model Accuracy: ", result_lr, "%")
LDA Model Accuracy: 100.0 %
LDA est meilleur que LogisticRegression sur les donnée avec class déséquilibrées. Si on n’avait pas fait le stratifié quand on sépare le train / test, le résultat de LR sera pire.
22) À quoi correspond la variable coef_ du modèle ? intercept_ ?
- coef_ et intercept_ du LDA
lda.coef_
array([[-16.82505403, -15.10324333]])
lda.intercept_
array([34.31369331])
- coef_ et intercept_ du logestic regression
lr.coef_
array([[-37.49209741, -3.41079322]])
lr.intercept_
array([30.75276672])
coef_ intercept_ défini le hyperplan qui sépare les données.
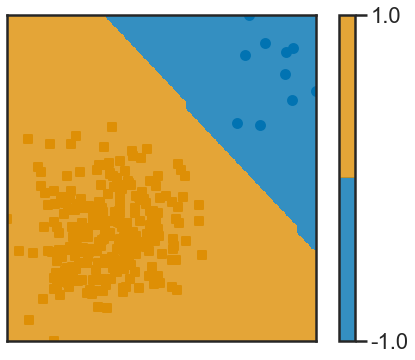
23) Utiliser la fonction frontiere_new pour visualiser la frontière de décision.
def f(x): return lr.predict(x.reshape(1, -1))
frontiere_new(f, X1, y1, w=None, step=50, alpha_choice=1,
colorbar=True, samples=True)
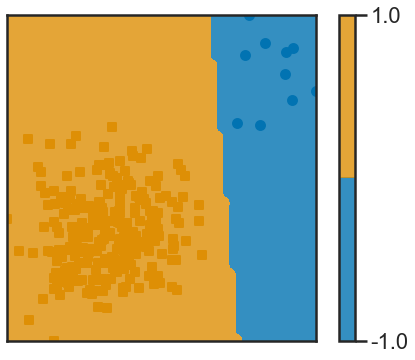
def f(x): return lda.predict(x.reshape(1, -1))
frontiere_new(f, X1, y1, w=None, step=50, alpha_choice=1,
colorbar=True, samples=True)
24) Appliquez la classification par régression logistique à des données issues de la base digits. Comme précédemment, coupez l’échantillon en deux parties de même taille et utilisez la première partie pour l’apprentissage et la deuxième pour tester. Indiquez le taux d’erreur.
from sklearn import metrics
def split_data(X, y):
return [
X[::2],
y[::2],
X[1::2],
y[1::2],
]
X_train, y_train, X_test, y_test = split_data(digits.data, digits.target)
lr = LogisticRegression(solver='liblinear', C=1e9,
multi_class='auto').fit(X_train, y_train)
y_pred = lr.predict(X_test)
print("Number of elements in test sample:", len(y_test))
print("Errors rate:", 1-accuracy_score(y_pred, y_test))
print((metrics.classification_report(y_test, lr.predict(X_test))))
Number of elements in test sample: 898
Errors rate: 0.08908685968819596
precision recall f1-score support
0 0.96 0.97 0.96 88
1 0.81 0.93 0.87 89
2 0.95 0.95 0.95 91
3 0.90 0.91 0.91 93
4 0.89 0.95 0.92 88
5 0.91 0.93 0.92 91
6 0.98 0.98 0.98 90
7 0.93 0.95 0.94 91
8 0.86 0.80 0.83 86
9 0.92 0.74 0.82 91
accuracy 0.91 898
macro avg 0.91 0.91 0.91 898
weighted avg 0.91 0.91 0.91 898
plt.figure(figsize=(12, 7))
sns.heatmap(metrics.confusion_matrix(
y_test, y_pred), annot=True)
plt.title('Confusion_matrix', y=1.05, size=15)
Text(0.5, 1.05, 'Confusion_matrix')